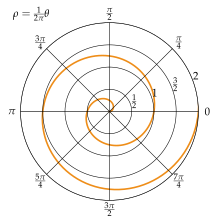
Архимедова спираль

Архимедова спираль

Архимедова спираль в полярной системе координат

Резьб (также арифметическая спиральная ) является самым простым из всех спиралей. Она возникает , когда радиус возрастает пропорционально до угла поворота во время вращательного движения : ${\ displaystyle r}$ ${\ displaystyle \ varphi}$

${\ Displaystyle г = а \ cdot \ varphi}$

с . ${\ displaystyle a> 0}$

характеристики

Представление в виде кривой параметров в декартовых координатах :

${\ Displaystyle е \ двоеточие \ varphi \ mapsto (r \, \ cos \ varphi, r \, \ sin \ varphi) = (a \, \ varphi \, \ cos \ varphi, a \, \ varphi \, \ sin \ varphi)}$.

Длина дуги от до IS ${\ displaystyle \ \ varphi _ {1}}$${\ displaystyle \ varphi _ {2}}$

${\ displaystyle {\ frac {a} {2}} \ left [\ varphi \, {\ sqrt {1+ \ varphi ^ {2}}} + \ ln \ left (\ varphi + {\ sqrt {1+ \ varphi ^ {2}}} \ right) \ right] _ {\ varphi _ {1}} ^ {\ varphi _ {2}}}$

или коротко: ${\ displaystyle {\ frac {a} {2}} \ left [\ varphi \, {\ sqrt {1+ \ varphi ^ {2}}} + \ operatorname {arsinh} \ varphi \ right] _ {\ varphi _ {1}} ^ {\ varphi _ {2}}}$

Таким образом, общая длина спирали от до составляет ${\ Displaystyle \ varphi _ {1} \ = \ 0}$${\ Displaystyle \ varphi _ {2} \ = \ \ varphi}$

${\ displaystyle {\ frac {a} {2}} \ left [\ varphi \, {\ sqrt {1+ \ varphi ^ {2}}} + \ ln \ left (\ varphi + {\ sqrt {1+ \ varphi ^ {2}}} \ right) \ right].}$

Область включена в первой революции

${\ displaystyle {\ frac {4} {3}} \ pi ^ {3} a ^ {2},}$

а на n-м обороте площадь

${\ Displaystyle \ 8 (п-1) \ пи ^ {3} а ^ {2}}$

дополнительно входит.

Архимедова спираль с параметрами и шагом

Кривизна вычисляется следующим образом в зависимости от угла поворота :${\ displaystyle \ varphi}$

${\ displaystyle \ kappa = {\ frac {\ varphi ^ {2} +2} {а (\ varphi ^ {2} +1) ^ {\ tfrac {3} {2}}}}}$

В дополнение к приведенному выше представлению в виде кривой параметров , спираль Архимеда также может быть описана как уравнение :

${\ displaystyle \ tan \ left ({\ frac {\ sqrt {x ^ {2} + y ^ {2}}} {a}} \ right) = {\ frac {y} {x}}}$

«Расстояние между обмотками»

Каждый луч, исходящий из начала координат, пересекает последовательные витки архимедовой спирали в точках с постоянным расстоянием (см. Рисунок справа). Отсюда и появился термин «арифметическая спираль». ${\ Displaystyle \ г = а \, \ varphi \}$ ${\ Displaystyle а \ cdot 2 \, \ пи \}$

Касаясь спирали, красные дорожки имеют одинаковую длину.

Это особое свойство спирали Архимеда часто выражается в том, что шаг ее витков постоянен. Однако такой способ выражения легко может быть неправильно понят, поскольку речь идет не о постоянном расстоянии между кривыми в смысле параллельных кривых . Спираль которого витки на самом деле имеет постоянное расстояние в последнем смысле была бы эвольвентная окружность .

Касательная собственность

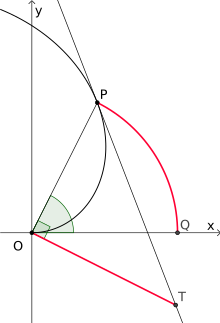
Есть точка P с соответствующим радиусом OP и углом поворота . Касательной к спирали через Р затем пересекает перпендикулярную к OP , установленной в О в точке Т. Тогда дуга окружности PQ , принадлежащие к углу поворота находится ровно до тех пор , как сегмента OT, то есть, применимо следующее:${\ displaystyle \ varphi}$${\ displaystyle \ varphi}$

${\ displaystyle \ angle POT = 90 ^ {\ circ} \, \ Rightarrow \, | {\ widehat {PQ}} | = | OT |}$

Возведение круга в квадрат и разделение углов

Угловое деление на три (n = 3): ${\ displaystyle \ beta = {\ tfrac {\ alpha} {3}}}$

Круговая квадратура по Архимеду

Квадратура круга: F (круг (M, r)) = F (ABCD) = F (CJHG)

Благодаря своему определению, согласно которому расстояние точки кривой от начала координат пропорционально углу поворота, спираль Архимеда подходит для деления угла на n равных частей и для возведения окружности в квадрат . Следовательно, это и трисектриса (n = 3), и квадрикс . Обе проблемы не могут быть решены с помощью циркуля и линейки , но если спираль Архимеда допущена в качестве единственной дополнительной помощи, то они могут быть решены.

Чтобы разделить угол BAC на n равных частей, сначала создается спираль Архимеда над его участком AB. Нога здесь действует как ось x с угловым наконечником A как начало координат . Расстояние от острия уголка до точки D пересечения  спирали с другим участком угла теперь разделено на n частей равной длины. С помощью теоремы о лучах это можно сделать только с помощью циркуля и линейки , так как для этого проводят следующий луч от углового наконечника A и проводят на n равных расстояниях от углового наконечника с помощью циркуля. Затем соединяют конечную точку последнего пути с точкой D и отрезками угла и проводят параллели этому маршруту через n-1, дальнейший путь заканчивается на балке угловой вершины A. Точки пересечения параллелей с отрезком угла AC разделите отрезок AD на n отрезков равной длины. Теперь вы строите n-1 окружностей, которые имеют точку угла A в качестве центра и проходят через n-1 конечные точки сегментов AD. Наконец, соединяют n-1 точек пересечения n-1 окружностей со спиралью с угловым наконечником A, и, таким образом, получается разделение угла BAC на n равных углов.

Чтобы возвести окружность в квадрат с радиусом r, сначала постройте две взаимно перпендикулярные оси координат через его центральную точку  M и создайте спираль Архимеда в этой системе координат . В спираль пересекает ось у в точке  Е , а длина в сегменте МЕ является единицы длины, так как связанного угла поворота спирали есть. Тогда прямоугольник с диаметром окружности 2r имеет длину и | ME | та же площадь, что и круг . Затем с помощью теоремы Евклида о высоте прямоугольник можно преобразовать в квадрат той же площади .${\ displaystyle {\ tfrac {r \ pi} {2}}}$${\ displaystyle {\ tfrac {\ pi} {2}}}$

Сам Архимед использовал другой метод, чтобы возвести круг в квадрат . Сначала он построил спираль за один полный оборот в системе координат с началом O, так что эта положительная половина оси x пересекается в P. Тангенс спирал в точке Р пересекает ось ординат в Т и прямоугольный треугольник OPT равен по площади к окружности с центральной O и радиусом OP. Этот треугольник можно легко преобразовать в прямоугольник той же площади, разделив пополам один из двух катетов , который можно преобразовать в квадрат с той же площадью, что и выше, с помощью теоремы Евклида о высотах .

Исторический

Архимед описал названную в его честь спираль в 225 г. до н. Э. В его трактате о спиралях , но он был уже известен его другу и современнику Конону из Самоса , который считается его первооткрывателем. Он был исследован Паппом в 4 веке нашей эры . Общее определение длины спирали было сделано Исааком Барроу в 1670 году.

Обобщения

Существуют различные обобщения спирали, первоначально описанной Архимедом , для которой спирали Архимеда часто используются как собирательный термин в литературе. Здесь исходное уравнение расширено до с . Ибо получается обычная спираль Архимеда. Падение также известно как спираль Ферма , падение - спираль литууса, а падение - гиперболическая спираль . В целом эти спирали могут существенно отличаться от исходной спирали Архимеда по свойствам и внешнему виду. ${\ Displaystyle г = а \, \ varphi}$${\ Displaystyle г = б + а \, \ varphi ^ {\ tfrac {1} {d}}}$${\ displaystyle d \ in \ mathbb {R}}$${\ displaystyle d = 1, \, b = 0}$${\ displaystyle d = 2, \, b = 0}$${\ displaystyle d = -2, \, b = 0}$${\ displaystyle d = -1, \, b = 0}$

Приложения

Лакричные улитки в форме архимедовой спирали

Рекорды как приложение спиралей Архимеда

Многие носители информации используют, по крайней мере, приблизительно принцип архимедовой спирали, поэтому ленты для хранения (например, аудио- и видеокассеты ) сворачиваются в виде спирали. Дорожки на пластинках или компакт-дисках также расположены в форме архимедовой спирали, что позволяет считывающей головке читать любой объем данных линейно ( последовательно ), не прерывая смены дорожки .

Жесткие диски для произвольного доступа , однако использовать с начала блоков / круговых сегментов на концентрически расположенных кругах .

литература

• Д. Д. Соколов: Спираль Архимеда . В энциклопедии математики , том 1, с. 240
• Клауди Альсина, Роджер Б. Нельсен: Очаровательные доказательства: Путешествие в элегантную математику . MAA 2010, ISBN 978-0-88385-348-1 , стр. 145-146 ( отрывок (Google) )
• Янош Акзель, Клауди Альсина: Трисекция углов, классические кривые и функциональные уравнения . Математический журнал, Том 71, № 3 (июнь 1998 г.), стр. 182-189 ( JSTOR 2691201 )
• Александр Остерманн, Герхард Ваннер: Геометрия по ее истории . Springer, 2012, ISBN 978-3-642-29163-0 , стр. 81-82
• Мидхат Дж. Газале: Гномон: от фараонов до фракталов . Princeton University Press, 1999, ISBN 978-0-691-00514-0 , стр. 168-171
• Мартин Гарднер: Неожиданное зависание и другие математические отклонения . University of Chicago Press, 1969, стр. 103-107.

веб ссылки

• Эрик В. Вайсштейн : Архимедова спираль . В: MathWorld (английский).
• Джон Дж. О'Коннор, Эдмунд Ф. Робертсон :  Спираль Архимеда. В: Архив истории математики MacTutor .

Индивидуальные доказательства

1. ↑ ^{а б} Дж. В. Раттер: Геометрия кривых . CRC Press, 2000, с. 71
2. ↑ Дитмар Херрманн: Древняя математика: история греческой математики, ее проблемы и решения . Springer, 2014, ISBN 978-3-642-37612-2 , стр. 181-187
3. ^ JW Rutter: Геометрия кривых . CRC Press, 2000, с. 149
4. ^ ^{A b} Александр Остерманн, Герхард Ваннер: Геометрия его историей . Springer, 2012, ISBN 978-3-642-29163-0 , стр. 81-82
5. ^ ^{A b} Клауди Альсина, Роджер Б. Нельсен: Очаровательные доказательства: Путешествие в элегантную математику . MAA 2010, ISBN 978-0-88385-348-1 , стр. 145-146 ( отрывок (Google) )
6. ↑ Жан-Поль Делахай: π - История . Springer, 2013 г., ISBN 978-3-0348-5085-8 , стр. 75