В линеаризация , нелинейные функции или нелинейные дифференциальные уравнения аппроксимируются с помощью линейных функций или линейных дифференциальных уравнений . Линеаризация используется потому, что линейные функции или линейные дифференциальные уравнения могут быть легко вычислены, а теория более обширна, чем для нелинейных систем.
касательная
Самый простой метод линеаризации - провести касательную на графике. Затем параметры касательной могут быть считаны, и полученная линейная функция ( форма точечного наклона прямой)
аппроксимирует исходную функцию вокруг точки . Это увеличение балла .
Если функция имеет аналитическую форму, уравнение касательной можно задать напрямую.
Относительная погрешность приближения составляет
К функции применимо, например, следующее:
Определение касательной соответствует определению линейного члена полинома Тейлора функции, которую нужно аппроксимировать.
Приложения
Линеаризация используется, помимо прочего, в области электротехники и управление инженерией для приближенного описания нелинейных систем с помощью линейных систем .
Результатом сетевого анализа может быть нелинейная система уравнений. При определенных условиях это может быть преобразовано в линейную систему уравнений . Не единственный, но самый простой метод линеаризации - это линеаризация в рабочей точке (сокращенно «AP»). Только это описано в следующих разделах.
Линеаризация умножения
На схеме потока сигналов сложные системы могут быть представлены блок- схемой, которая используется для качественной визуализации математических моделей.
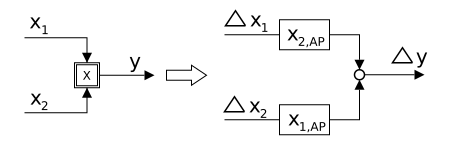
Если на этой схеме потока сигналов есть точка умножения, ее можно преобразовать в точку сложения путем линеаризации.
Далее мы обозначаем произведением двух чисел и :
В рабочей точке мы можем линеаризовать умножение, записав как сумму рабочей точки и разницы :
Мы можем умножить этот продукт согласно закону распределения . В результате получается сумма:
Предположим теперь, что соотношение отклонений от рабочей точки и самой рабочей точки невелико:
и таким образом продукт тоже маленький. Таким образом, линеаризованное умножение :
пример
Выберите числа:
Теперь возникает вопрос, как выбрать рабочие точки. Для упрощения расчетов, мы округляем вверх , и к Избери: от
линеаризованного продукта настолько
с ошибкой .
Линеаризация деления
Линеаризация деления, показанного на схеме потока сигналов
Теперь рассмотрим частное двух чисел и :
Так же, как и при умножении, мы развиваемся вокруг рабочей точки . При этом мы можем записать частное следующим образом:
Исключение операционных точек дает на разделение:
Теперь мы хотим линеаризовать числитель и знаменатель дроби. Для этого воспользуемся геометрическим рядом . Следующее применяется к нулевой последовательности :
Здесь в соответствии с выбором.
Вставка обеспечивает линеаризацию
Знаменатель приведенной выше дроби можно линеаризовать аналогичным образом. Линеаризуется деление можно записать в виде:
Линеаризация обыкновенных дифференциальных уравнений
Хорошо известным примером линеаризации нелинейного дифференциального уравнения является маятник . Уравнение:
Нелинейная часть есть . Для небольших колебаний вокруг рабочей точки это приблизительно равно :
К рабочей точке относится следующее:
-
и, таким образом, линеаризованное дифференциальное уравнение
-
.
Эти линеаризованные дифференциальные уравнения обычно намного проще решить. Для математического маятника (выберите ) уравнение может быть решено с помощью простых экспоненциальных функций, в то время как нелинейное уравнение не может быть решено аналитически. Дополнительные сведения о линеаризации дифференциальных уравнений описаны в статье о представлении в пространстве состояний .
Касательная плоскость
Представление в виде плана потока сигналов
Если данная функция должна быть линеаризована в какой-то точке , используется формула Тейлора . Результат соответствует касательной плоскости в этой точке.
Следующее относится к функции в непосредственной близости от точки :
Пример:
приводит к касательной плоскости
Смотри тоже
веб ссылки
