Медиана

В статистике , то медиана - также называется центральное значение - это среднее значение и параметр позиции . Медиана измеренных значений в исходном списке - это измеренное значение, которое находится точно «посередине» при сортировке измеренных значений по размеру. Например, для неупорядоченного исходного списка 4, 1, 37, 2, 1 измеренное значение 2 является медианным, а центральное значение в упорядоченном исходном списке - 1, 1,  2 , 4, 37.

Как правило, медиана делит набор данных, выборку или распределение на две равные части, так что значения в одной половине не превышают медианное значение, а другая половина не меньше.

описание

Медиана делит список значений на две части. Определить его можно следующими способами:

• Все значения упорядочены (в порядке возрастания).
• Если количество значений нечетное, среднее число является медианным.
• Если количество значений четное, медиана обычно определяется как среднее арифметическое двух средних чисел, которые затем называются нижней и верхней медианой .

Важное свойство медианы - устойчивость к выбросам .

• Пример: семь несортированных измеренных значений 4, 1, 15, 2, 4, 5, 4 отсортированы по размеру: 1, 2, 4, 4 , 4, 5, 15; Медиана (включая верхнюю и нижнюю медианы) - это среднее значение, т.е. 4. Если в примере из-за ошибки 4 было заменено на 46, медиана не изменится: 1, 2, 4, 4 , 5 , 15, 46. Среднее арифметическое, напротив, подскакивает с 5 до 11.

Сравнение с другими показателями центральной тенденции

Сравнение между модой, медианой и «средним» (на самом деле: ожидаемым значением ) двух логнормальных распределений с медианой 1

Медиана особый квантиль , а именно ¹ / ₂ -quantile. Другими важными показателями положения являются среднее арифметическое и мода .

По сравнению со средним арифметическим, часто называемым средним, медиана более устойчива к выбросам (чрезвычайно отклоняющиеся значения) и также может применяться к переменным, масштабируемым по порядку . Термин медиана (от латинского medianus , `` посередине '', `` средний '') происходит от геометрии , где также обозначает границу между двумя половинами одинакового размера.

Области применения

Среднее значение этой таблицы оценок - 3−. Чуть меньше половины результатов хуже; добавляя саму оценку 3-, она просто превышается наполовину.

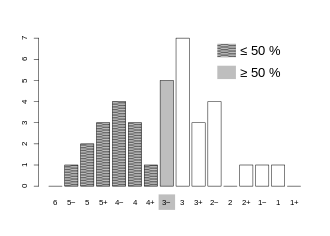
В отличие от среднего арифметического, медиана также может использоваться для переменных с обычной шкалой, таких как классы, для которых нет количественной разницы. Но медиана может также использоваться для интервальных и ratio- масштабируемых данных , а затем имеет свои недостатки и преимущества по сравнению с средним арифметическим как мера позиции. Медиана не может использоваться только для номинально масштабируемых переменных, характеристики которых не имеют естественного ранжирования, таких как переменная страна рождения . Здесь значение режима - единственная мера положения, которую можно определить.

Медиана используется в статистике и теории вероятностей в трех различных значениях:

1. в качестве меры по позиции в описательных статистиках для описания списка бетона выборки значений .
2. в теории вероятностей как медиана распределения вероятностей или случайной величины . Здесь медиана является альтернативой ожидаемому значению для указания «среднего значения».
3. в математической статистике как медиана случайной выборки для надежной оценки неизвестных распределений.

Медиана выборки

Значение - это медиана выборки, если по крайней мере половина элементов выборки не больше, а по крайней мере половина не меньше . ${\ displaystyle m}$${\ displaystyle m}$${\ displaystyle m}$

Если вы отсортируете значения наблюдений по размеру, то есть если вы перейдете к случайной выборке, упорядоченной по рангу , медиана для нечетного числа наблюдений будет значением наблюдения в середине этой последовательности . При четном количестве наблюдений нет единого среднего элемента, а есть два. Здесь значения двух средних наблюдений и все промежуточные значения (хотя они, возможно, не встречались ни в одном из наблюдений) являются медианами выборки, поскольку вышеуказанное условие применяется ко всем этим значениям.

В случае кардинально масштабированных измеренных значений (если имеет смысл вычислить разницу между измеренными значениями) обычно используется среднее арифметическое двух средних наблюдаемых значений в случае четного числа наблюдений. Медиана упорядоченного образца из измеренных значений , то ${\ displaystyle {\ tilde {x}}}$${\ displaystyle (x_ {1}, x_ {2}, \ dotsc, x_ {n})}$${\ displaystyle n}$

${\ displaystyle {\ tilde {x}} = {\ begin {case} x_ {m + 1} & {\ text {для нечетных n = 2m + 1}} \\ {\ frac {1} {2}} ( x_ {m} + x_ {m + 1}) & {\ text {для четных n = 2m}} \ end {case}}}$

Это определение имеет то преимущество , что, в случае образцов из симметричных распределений, средние арифметические и медиана в ожидаемых величинах одинаковы.

Верхняя и нижняя медиана

Часто нужно убедиться, что медиана является частью выборки. В этом случае, в качестве альтернативы приведенному выше определению, если есть четное число элементов, либо нижний средний или верхний медиана выбран в качестве медианы . В случае нечетного количества наблюдений, конечно, то же самое, что и выше . ${\ displaystyle n = 2m}$${\ displaystyle {\ tilde {x}} _ {u} = x_ {m}}$${\ Displaystyle {\ тильда {х}} _ {о} = х_ {м + 1}}$${\ Displaystyle п = 2 м + 1}$${\ displaystyle {\ tilde {x}} = {\ tilde {x}} _ {u} = {\ tilde {x}} _ {o} = x_ {m + 1}}$

С помощью гауссовых скобок индексы также могут быть относительно компактно выражены сами по себе: ${\ displaystyle n}$

${\ displaystyle {\ tilde {x}} _ {u} = x _ {\ left \ lfloor {\ frac {n + 1} {2}} \ right \ rfloor}}$

${\ displaystyle {\ tilde {x}} _ {o} = x _ {\ left \ lceil {\ frac {n + 1} {2}} \ right \ rceil}}$

Это определение медианы играет важную роль в системах баз данных , например , таких как Б. в запросах SELECT с использованием медианы медиан.

характеристики

Медиана и, в случае четного числа измеренных значений, все значения с минимизируют сумму абсолютных отклонений, то есть для любого применяется ${\ displaystyle {\ tilde {x}}}$${\ displaystyle {\ tilde {x}}}$${\ displaystyle {\ tilde {x}} _ {u} \ leq {\ tilde {x}} \ leq {\ tilde {x}} _ {o}}$${\ displaystyle x}$

${\ displaystyle \ sum _ {i = 1} ^ {n} | {\ tilde {x}} - x_ {i} | \ leq \ sum _ {i = 1} ^ {n} | x-x_ {i} |.}$

Медиана является основой метода наименьших абсолютных отклонений и метода робастной регрессии . Среднее арифметическое, с другой стороны, сводит к минимуму сумму квадратов отклонений , является основой метода наименьших квадратов и регрессионного анализа, и его математически легче обрабатывать, но оно не устойчиво к выбросам.

Как описано выше, медиана может быть определена алгоритмически путем сортировки измеренных значений. Обычно это связано с трудозатратами , возможно только для специальных классов входных данных (см. Алгоритм сортировки ). Но есть также алгоритмы для определения квантилей с линейным усилием наихудшего случая и алгоритмы для оценки, например, метод Корниша-Фишера . ${\ Displaystyle \ Omega (п \ журнал п)}$${\ Displaystyle {\ mathcal {O}} (п)}$${\ Displaystyle {\ mathcal {O}} (п)}$

Медиана сгруппированных данных

Пирамида населения Танзании 2016, медиана оценивается в 18 лет

В частности, в социальных науках медиана часто оценивается для статистики, поскольку не все данные даны явно и точно, а доступны только сгруппированными по интервалам . Например, опросы редко спрашивают о точной заработной плате, а только о классе дохода, то есть диапазоне, в котором находится заработная плата. Если известны только частоты каждого класса, то медиана такой выборки обычно может быть определена только приблизительно. Пусть это будет количество всех данных, соответствующее количество данных -й группы и / или соответствующие верхние или нижние пределы интервала. Сначала определяется средний класс (или медианная группа ), т.е. то есть та группа, в которую попадает медиана (согласно вышеприведенному общепринятому определению), например Б. -я группа. Количество определяется тем, что , но держится. Если не дается никакой дополнительной информации о распределении данных, z. B. Постулируемое равномерное распределение, так что линейная интерполяция может использоваться в качестве вспомогательного средства для получения оценки медианы сгруппированных данных: ${\ displaystyle n}$${\ displaystyle n_ {i}}$${\ displaystyle i}$${\ displaystyle u_ {i}}$${\ displaystyle o_ {i}}$${\ displaystyle m}$${\ displaystyle m}$${\ displaystyle \ textstyle \ sum _ {k = 1} ^ {m-1} n_ {k} <{\ frac {n} {2}}}$${\ displaystyle \ textstyle \ sum _ {k = 1} ^ {m} n_ {k} \ geq {\ frac {n} {2}}}$

${\ displaystyle x _ {\ mathrm {med}} = u_ {m} + {\ frac {{\ frac {n} {2}} - \ sum \ limits _ {k = 1} ^ {m-1} n_ {k}} {n_ {m}}} \ cdot (o_ {m} -u_ {m})}$

Если не дается никакой дополнительной информации о распределении данных, любое другое распределение, кроме равномерного, также может существовать, и, таким образом, любое другое значение в -м интервале также может быть медианным. ${\ displaystyle m}$

В отличие от обычного определения медианы, она не обязательно должна быть элементом фактического объема данных, который обычно даже не известен.

пример

Доход :

Класс ( ) ${\ displaystyle i}$	Диапазон ( до ) ${\ displaystyle u_ {i}}$${\ displaystyle o_ {i}}$	Размер группы ( ) ${\ displaystyle n_ {i}}$
1	не менее 0, менее 1500	160
2	не менее 1500, менее 2500	320
3	не менее 2500, менее 3500	212

Рассчитать

${\ displaystyle {\ tfrac {n} {2}} = {\ tfrac {212 + 320 + 160} {2}} = {\ tfrac {692} {2}} = 346.}$

Таким образом, медиана находится во 2-м классе (т.е. ), поскольку в первом классе всего 160 элементов. Это приводит к оценке медианы ${\ displaystyle m = 2}$

${\ displaystyle x _ {\ mathrm {med}} = 1500 + {\ tfrac {346-160} {320}} \ cdot (2500-1500) = 2081 {,} 25.}$

Поскольку конкретное распределение данных в интервалах неизвестно, любое другое значение во 2-м интервале также может быть медианным. Следовательно, значение 2081,25, вычисленное в качестве примера, может быть до 581,25 слишком большим и до 418,75 слишком маленьким, поэтому ошибка оценки может достигать 28%.

Иллюстрацией этой процедуры определения медианы для сгруппированных данных является графическое определение с помощью кумулятивной кривой . Здесь ищется значение абсциссы , принадлежащее значению ординаты . Если значение меньше и четно, вместо него также можно выбрать значение ординаты . ${\ Displaystyle х _ {\ mathrm {med}}}$ ${\ Displaystyle {\ tfrac {п} {2}}}$${\ displaystyle n}$${\ displaystyle {\ tfrac {n} {2}} + 1}$

Другие варианты

• Функция благосостояния является альтернативой медиане при определении массового дохода по заданному распределению доходов.
• Другой способ справиться с экстремальными значениями, отличными от медианы, - использовать усеченное среднее , которое получается путем удаления наименьшего и наибольшего значений перед вычислением (обычно 5% значений опускаются).
• Батлер также имеет более строгое определение медианы (которое встречается реже), в котором говорится, что медиана - это значение, для которого количество меньших значений в серии равно количеству больших значений в серии . Для особых случаев, таких как 3, 3, 3, 3, 4 или 1, 2, 3, 3, 3, существует процедура, с помощью которой может быть вычислена четкая медиана при сохранении более строгого определения.

Медиана и среднее арифметическое: очень простой пример

В группе из десяти человек у всех разный ежемесячный доход. Один человек получает 1 000 000 евро, остальные девять получают от 1 000, 2 000, 3 000 евро и т. Д. До 9 000 евро.

Среднее арифметическое, «среднее» - ежемесячный доход каждого из десяти человек с суммой всех доходов, равномерно распределенных между ними, - в данном случае составляет 104 500 евро. Однако только один из десяти человек зарабатывает больше, а остальные девять значительно меньше.

С другой стороны, медиана составляет 5 500 евро. Пять человек зарабатывают больше, пять человек меньше. Медиана отмечает границу между более высокой и низкооплачиваемой половиной.

веб ссылки

Викисловарь: Медиана  - объяснение значений, происхождение слов, синонимы, переводы

Викиучебники :: Математика для школы${\ displaystyle {\ begin {smallmatrix} {\ mathbf {MATH} \ mu \ alpha T \ mathbb {R} ix} \ end {smallmatrix}}}$  - Параметры местоположения

• Подробные пояснения по вычислению медианы на «тропинке»: Викиучебники
• Использование устойчивых свойств медианы на примере кругового уравнивания. ( Памятка от 2 апреля 2010 г. в Интернет-архиве ).
• Эрик В. Вайсштейн : статистическая медиана . В: MathWorld (английский).
• А. В. Прохоров: Медиана (в статистике) . В: Michiel Hazewinkel (Ed.): Encyclopedia of Mathematics . Springer-Verlag и EMS Press, Берлин 2002, ISBN 978-1-55608-010-4 (английский, онлайн ). Ошибка в шаблоне: "Литература" - *** Недействительно: недопустимые скобки в скобках.

Индивидуальные доказательства

1. ↑ Ганс Лоннингер: Основы статистики. Имею ввиду .
2. ↑ Кристофер Батлер: Статистика в лингвистике . 1985 г. 
3. ↑ Центральная тенденция. (Больше не доступны в Интернете.) Архивировано из оригинала на 16 января 2013 года ; Доступ к 9 мая 2016 года .