Точечная симметрия

Направляйте симметричные объекты на плоскости

Симметрии точки, также инверсия симметрия или центральная симметрия , находятся в геометрии в свойстве фигуры . Фигура является точечно-симметричной, если она отображается на себя путем отражения в точке симметрии .

определение

(Плоская) геометрическая фигура (например, квадрат) называется точечно-симметричной, если существует точечное отражение, изображающее эту фигуру на себе. Точка, в которой происходит это зеркальное отражение, называется центром симметрии .

Зеркальное отображение точки как вращение (и зеркальное отображение)

На плоскости (двумерное евклидово пространство ) точечное отражение соответствует повороту геометрической фигуры на 180 ° вокруг точки симметрии. Здесь точечная симметрия - это частный случай вращательной симметрии . В трехмерном евклидовом пространстве точка отражения соответствует повороту геометрической фигуры на 180 ° вокруг точки симметрии и последующему отражению на плоскости, перпендикулярной оси вращения, через точку симметрии.

Следующее применяется в более общем плане:

В 2N-мерном пространстве точечное отражение соответствует N поворотам на 180 ° в каждом случае. Оси вращения попарно перпендикулярны друг другу и пересекаются в точке симметрии.

В 2N + 1-мерном пространстве точечное отражение соответствует N поворотам на 180 ° и последующему отражению. Оси вращения попарно перпендикулярны друг другу и пересекаются в точке симметрии. Точка симметрии также находится в плоскости зеркала, и все оси вращения перпендикулярны плоскости зеркала.

Примеры

• В случае квадрата точечная симметрия (сама по себе) существует тогда и только тогда, когда это параллелограмм . Центр симметрии - это пересечение диагоналей. Как частные случаи параллелограмма, прямоугольник , ромб и квадрат являются точечно-симметричными.
• Каждый круг (сам по себе) точечно-симметричен относительно своего центра.
• Два круга с одинаковым радиусом точечно симметричны друг другу. Центр симметрии - это середина соединительной линии между двумя центрами окружностей.
• Центров симметрии может быть только несколько, если фигура не ограничена . Самый простой пример - прямая линия. У него даже бесконечное количество центров симметрии.
• Треугольник никогда не точка , симметричная. Однако два треугольника могут быть точечно симметричными друг другу.
• Правильный многоугольник с четным числом углов является точкой-симметричной.

Точечная симметрия графиков функций

обзор

График точечной симметричной функции

Общая задача школьного курса математика, чтобы доказать , что график данной функции является точкой симметричной с областью определения и с реальными значениями функции. ${\ displaystyle f \ двоеточие D \ to \ mathbb {R}}$ ${\ Displaystyle D \ подмножество \ mathbb {R}}$

Если есть точка, значит уравнение для функции${\ Displaystyle (а, б),}$${\ displaystyle f}$

${\ displaystyle f (a + x) -b = -f (ax) + b}$

выполняется для всех , то функция точечно-симметрична относительно точки. Указанное условие выполняется с ${\ displaystyle x \ in D}$${\ displaystyle (a, b).}$

${\ Displaystyle f (x) = 2b-f (2a-x)}$

эквивалент, как показывает подстановка . В частном случае точечной симметрии относительно начала координат это уравнение упрощается до ${\ Displaystyle х \ к ха}$${\ displaystyle (0,0)}$

${\ Displaystyle f (-x) = - f (x).}$

Если это верно для всех , то есть точечная симметрия относительно начала координат. Тогда функция называется нечетной . ${\ displaystyle x}$${\ displaystyle f}$

Примеры

Точечная симметрия относительно начала координат

Кривая f (x) = 2x ⁵

Учитывая функцию Then: ${\ displaystyle f (x) = 2x ^ {5}.}$

${\ Displaystyle f (-x) = 2 (-x) ^ {5} = 2 (-1) ^ {5} x ^ {5} = 2 (-1) x ^ {5} = - 2x ^ {5 } = - f (x)}$

Таким образом, график функции является точечно-симметричным с центром симметрии в начале координат (0,0).

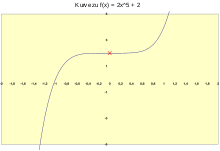
Точечная симметрия относительно точки (0,2)

Кривая f (x) = 2x ⁵ + 2

Учитывая функцию Select, а затем мы имеем: ${\ displaystyle f (x) = 2x ^ {5} +2.}$${\ displaystyle a = 0}$${\ displaystyle b = 2.}$

${\ Displaystyle 2b-f (2a-x) = 4-f (-x) = 4- (2 (-x) ^ {5} +2) =}$

${\ displaystyle = 4 - (- 2x ^ {5} +2) = 4 + 2x ^ {5} -2 = 2x ^ {5} + 2 = f (x)}$

Следовательно, график функции точечно симметричен относительно точки и выполняется ${\ displaystyle (0,2)}$

${\ displaystyle -f (x) + 2 = f (-x) -2.}$

Эта процедура не помогает определить точку симметрии . Однако в большинстве случаев достаточно построить график функции и вывести из него предположение о точке симметрии. ${\ displaystyle (0,2)}$

Индивидуальные доказательства

1. ↑ Артур Шенфлис: Кристаллические системы и кристаллическая структура . Teubner, Leipzig 1891 (XII, 638 с., Интернет-ресурсы ). 
2. ↑ Spektrum.de: Инверсионная симметрия. Проверено 5 марта 2020 года . 
3. ↑ Большой карманный словарь Мейера в 24 томах. BI-Taschenbuchverlag, 1992, том 21, с. 258.
4. ^ Арнфрид Кемниц: Математика в начале курса . Vieweg + Teubner, Висбаден 2011, ISBN 978-3-8348-8258-5 , стр. 144 .