Симметрия (геометрия)

Симметрия и асимметрия

симметрия

в архитектуре

в биологии

" Витрувианский человек " Леонардо да Винчи

Геометрический термин симметрия ( древнегреческая συμμετρία symmetria ровность, однородность , из σύν сина «вместе» и μέτρον Metron , мера) обозначает свойство , что геометрический объект может быть отображенным на себя через движение , то есть выводится в неизменном виде . Преобразование , которое отображает объект в себя называется симметрией отображение или симметрии операции .

Иногда два (или более) разных геометрических объекта считаются симметричными друг другу, если при совместном рассмотрении они образуют симметричную фигуру.

В зависимости от количества рассматриваемых измерений существуют следующие различные симметрии:

Симметрии в одномерном

В одномерный, то есть на одной прямой, существует симметрия по отношению к одной точке, а также от симметрии перевода (смещения).

Симметрии в двух измерениях

В двухмерном пространстве необходимо различать точечную и осевую симметрию . Кроме того, здесь также встречаются трансляционные симметрии.

Вращательная симметрия / вращательная симметрия

Четыре правильных многоугольника и две другие геометрические фигуры с ключевыми фигурами их вращательной симметрии, также называемой вращательной симметрией ( n = 1 означает: без вращательной симметрии)

Двумерная геометрическая фигура имеет свойство быть осесимметричной, когда фигура имеет центральную точку, и фигура отображается сама на себя, когда она вращается вокруг этой точки. Круг или круговое кольцо имеет осевую симметрию в смысле более узкого. Поворот на любой угол отображает его на себя.

Фигура также называется осесимметричной, если ее можно изобразить на самой себе, повернув ее вокруг центральной точки на фиксированный угол с 0 ° << 360 °. Угол поворота может быть определен только путем деления полного угла на величину производимого> 1, то есть . Это число является мерой вращательной симметрии и также называется «счетчик». Соответственно, эта симметрия также называется -множественной или -кратной вращательной симметрией (аналог английского « -кратная вращательная симметрия») или также « -множественной вращательной симметрией».${\ displaystyle \ varphi}$${\ displaystyle \ varphi}$${\ displaystyle n}$${\ displaystyle \ varphi = {\ frac {360 ^ {\ circ}} {n}}}$${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle n}$

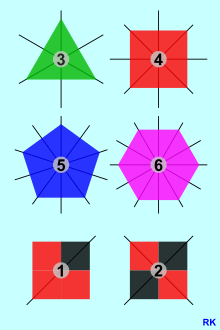
Правильные многоугольники - это типичные вращательно-симметричные фигуры. На графике справа показаны первые четыре, при этом также нанесен максимально возможный показатель вращательной симметрии. Кроме того, показаны еще две фигуры, а именно одна без и одна с двойной вращательной симметрией. В тривиальном случае нет вращательной симметрии / вращательной симметрии, и кодовое число 1 не используется в математическом контексте, если вы не хотите идентифицировать тривиальную циклическую группу , которая состоит только из идентичного отображения . ${\ displaystyle n}$${\ displaystyle n = 1}$ ${\ displaystyle C_ {1}}$

Симвология Шенфлиса определяет символ для элементов симметрии и групп симметрии вращательной симметрии . Другими примерами двойной вращательной симметрии являются точечно-симметричные фигуры, показанные ниже . Тот факт, что точечно-симметричные объекты всегда также симметричны относительно вращения, однако, применим только к двумерному. ${\ displaystyle C_ {n}}$

Зеркальная симметрия / осевая симметрия

Зеркальное отражение симметричных объектов на плоскости

Все элементы симметрии вышеуказанных многоугольников, включая их линии зеркальной симметрии

Зеркальной симметрии является формой симметрии, которая возникает , когда объекты перпендикулярно оси симметрии зеркального (см рисунок). В двухмерных терминах это синоним осевой симметрии или осевой симметрии . Следующая информация относится к каждой оси зеркального отображения:

1. Фигура и рисунок фигуры совпадают друг с другом.
2. Линия и линия изображения имеют одинаковую длину.
3. Угол обзора и угол обзора такие же.
4. Фигурка и фигуративная фигура имеют разные направления вращения при условии, что направление вращения определено на рисунке.

Примеры

• Треугольники могут иметь одну или три оси зеркальной симметрии: равнобедренный треугольник осесимметричен перпендикуляру к основанию. Однородные равносторонние треугольники имеют три оси зеркальной симметрии, как показано на рисунке напротив. Тот факт, что в этих многоугольниках, показанных в цвете, количество осей симметрии соответствует количеству, упомянутому выше для вращательной симметрии, в общем случае не применяется, потому что есть много вращательно-симметричных объектов, которые не имеют зеркальной симметрии, например, точечно-симметричные формы, показанные ниже .
• Четырехугольники могут иметь одну, две или даже четыре оси зеркальной симметрии:
  • По крайней мере, одна ось зеркальной симметрии имеет равнобедренные трапеции (через центры параллельных сторон) и квадраты дракона (по диагонали).
  • Есть как минимум две оси зеркальной симметрии для прямоугольника (перпендикуляры с противоположных сторон) и для ромба (обе диагонали).
  • Наконец, однородный квадрат представляет собой прямоугольник и ромб и имеет четыре оси зеркальной симметрии. Если он «заполнен», число можно уменьшить, как показано на соседнем графике.
• Круги и кольцевые кольца даже имеют бесконечное количество осей симметрии, поскольку они симметричны относительно каждой оси через центральную точку.
• Еще одна фигура с бесконечным числом осей симметрии - это прямая линия . Поскольку он бесконечно длинный, он симметричен относительно каждой оси, перпендикулярной ему, а также относительно оси, лежащей на самой себе.

Осевая симметрия графиков функций

График осесимметричной функции

Задача , которая особенно популярна в школе математику, чтобы доказать , ось симметрии для графика в функции . Эта проверка особенно проста в случае симметрии оси y (декартовой) системы координат . Функция аксиально симметрично к y- оси , если:

${\ Displaystyle е (-х) \, = \, е (х)}$

Если это верно для всех x, то имеется осевая симметрия, то есть f - четная функция .

Это условие сводится к тому, что значения функции для противоположно равных аргументов и должны совпадать. ${\ displaystyle x}$${\ displaystyle -x}$

В более общем плане применяется следующее: график функции f аксиально симметричен прямой линии с уравнением тогда и только тогда, когда следующее условие верно для любых значений x : ${\ Displaystyle х = а}$

${\ Displaystyle е (топор) \, = \, е (а + х)}$

Замена на дает эквивалентное условие: ${\ displaystyle x}$${\ displaystyle xa}$

${\ Displaystyle е (2а-х) \, = \, е (х)}$

Латинские заглавные буквы симметрии

Латинские заглавные буквы симметрии

На рисунке « Симметрии латинских заглавных букв» 26 букв разделены на пять групп в соответствии с их свойствами геометрической симметрии. Буквы FHJLPQR не имеют симметрии. НСЗ двояко осесимметричны. AMTUVWY симметричны вертикальной, а BCDEK - горизонтальной зеркальной линии. Наивысшая симметрия с четырьмя элементами симметрии показана буквами HIOX, которые имеют двойную вращательную симметрию и каждая из них имеет горизонтальную и вертикальную зеркальную линию.

В некоторых словах тоже существует геометрическая симметрия. Междометие В.Г.О., например, состоит из четырех элементов симметрии, OTTO имеет вертикальную и горизонтальную ЛПП зеркальной линии. Эти слова также являются словесными палиндромами . CEILING и HEIDE зеркально симметричны относительно горизонтальной прямой линии.

Точечная симметрия

Направляйте симметричные объекты на плоскости

Точки симметрии , а центральная симметрия , является свойством геометрических объектов. Геометрический объект (например, квадрат) называется (сам по себе) точечно-симметричным, если есть точечное отражение, которое отображает этот объект на самом себе . Точка, в которой происходит это зеркальное отражение, называется центром симметрии .

Примеры

• С квадратом существует точечная симметрия (сама по себе) тогда и только тогда, когда он является параллелограммом . Центр симметрии в этом случае - это пересечение его диагоналей. Как частные случаи параллелограмма, прямоугольник , ромб и квадрат также являются точечно-симметричными.
• Каждый круг (сам по себе) симметричен относительно своего центра.
• Два круга с одинаковым радиусом точечно симметричны друг другу. Центр симметрии - это середина соединительной линии между двумя центрами окружностей. В случае точечной симметрии симметричные друг другу линии всегда имеют одинаковую длину.

Точечная симметрия графиков функций

График точечной симметричной функции

Задача, которая особенно часто встречается в школьной математике, - доказать, что график заданной функции является точечно-симметричным. Это доказательство может быть представлено следующей формулой:

${\ displaystyle f (a + x) -b = -f (ax) + b}$.

Если это уравнение выполняется для всех x , то есть точечная симметрия относительно точки ( a, b ). В частном случае точечной симметрии относительно начала координат (0,0) это уравнение упрощается до:

${\ Displaystyle f (-x) = - f (x)}$.

Если это верно для всех x , то есть точечная симметрия относительно начала координат.

Поступательная симметрия

Трансляционно-симметричная решетка

Фигуры, которые превращаются в себя сдвигом или переносом (что не является тождеством), обладают трансляционной симметрией . Они также известны как периодические .

• Трансляционно-симметричные фигуры обязательно должны быть неограниченными. В математических приложениях этого практически никогда не бывает, поэтому ограниченные подмножества периодических множеств ( решетка , кристаллическая структура и т. Д.) Называются периодическими.
• Графики периодических действительных функций, таких как функция синуса, показывают симметрию сдвига в одном направлении.

В сетке с базисными векторами каждая точка может быть достигнута вектором трансляции на целые значения . Угол между ними произвольный. Базисные векторы также являются векторами переходов и вместе образуют так называемую элементарную ячейку .${\ displaystyle {\ vec {\ alpha}}, {\ vec {\ beta}}, {\ vec {\ gamma}}}$${\ displaystyle {\ vec {T}}}$${\ displaystyle u, v, w}$${\ displaystyle {\ vec {\ alpha}}, {\ vec {\ beta}}, {\ vec {\ gamma}}}$

${\ displaystyle {\ vec {T}} = u * {\ vec {\ alpha}} + v * {\ vec {\ beta}} + w * {\ vec {\ gamma}}}$

Масштабная симметрия

В некоторых математических и физических контекстах неизменность объекта при увеличении или уменьшении называется масштабной симметрией или масштабной инвариантностью . Этот феномен становится очень очевидным в так называемых фракталах .

Симметрии в трех измерениях

Только срединная сагиттальная плоскость (срединная плоскость) тела билатерии является зеркальной плоскостью.

В природе

Симметрия иглокожих (пентамеризм) на примере морской звезды : пятикратная ось вращения и вертикальные зеркальные плоскости ( точечная группа C _5v по Schoenflies )

Телосложения подавляющего большинства видов животных , а также структура многих органов растений внешне почти зеркально симметричны , - говорится в биологии , как симметричны - с левой и правой половины. Единственная плоскость симметрии (моносимметрии) - это анатомическая срединная плоскость , то есть срединная (расположенная в центре) сагиттальная плоскость; это все уровни тела, простирающиеся спереди назад и сверху вниз. 95 процентов всех видов животных, включая человека, являются bilateria («двусторонние животные») с одноименной симметрией тела (другие, очень оригинальные животные (например, медузы ) часто обладают вращательной симметрией относительно продольной оси, их тело следовательно, приблизительный твердотельный оборот ). Благодаря моносимметрии билатерии можно определить четкие плоскости и направления тела, что упрощает анатомическое описание. Но симметрия тела не идеальна, поэтому многие просто возникающие (непарные) внутренние органы (например, сердце) исключены из зеркальной симметрии. Все части тела симметричной формы, например глаза , уши , руки , ноги , грудь и т. Д. Человека , имеют небольшие отклонения друг от друга по положению, форме и размеру.

В зоологии пятиконечная радиальная симметрия иглокожих , уникальная для Bilateria, называется пентамеризмом (то есть в случае морской звезды пять плоскостей симметрии проходят через центральную ось вращения). В математике свойства симметрии морских звезд можно описать вращающейся группой . ( Личинки морских звезд двусторонне симметричны, как и большинство других животных в группе. Пентамеризм развивается только во время метаморфоза .)

Без симметрии, т. Е. Асимметричный , без тканевого ( губки и плакозоа ).

Соответствует двумерным элементам симметрии

На оси симметрии в двумерных соответствует зеркальной симметрии относительно плоскости в трехмерное. Точки симметрия в двумерный соответствует осевой симметрии (поворотная симметрия вокруг 180 °). Также существует точечная / центральная симметрия в пространстве и, как и в плоскости, трансляционная симметрия .

Вращательная симметрия / Вращательная симметрия

Обычные призмы с осями вращения и их счетчиками ( n = 1 означает: без вращательной симметрии)

Трехмерные объекты являются вращательно-симметричными в более узком смысле, если вращение вокруг любого угла вокруг оси (оси симметрии) отображает объект на себя. Этот тип вращательной симметрии относительно оси также известен как цилиндрическая симметрия . Трехмерные геометрические объекты с этим свойством также называют телами вращения.

Аналогично двумерному, концепция вращательной или вращательной симметрии также используется, когда тело может быть отображено на самом себе, вращаясь на определенные углы вокруг оси. В качестве примеров вращательно-симметричных трехмерных объектов призмы показаны в перспективе на графике напротив , которые возникают, когда двумерные многоугольники на графике над четырьмя правильными многоугольниками и двумя другими геометрическими фигурами с ключевыми фигурами их вращательной симметрии смещаются в пространстве вдоль прямая линия, перпендикулярная фигуре, становится. Эта процедура также называется выдавливанием многоугольника. Возникают прямые призмы, особые многогранники , которые в этом случае, если данные многоугольники являются правильными многоугольниками, называются правильными призмами.

Центр симметрии 2D-объекта становится осью вращения с острием стрелки через выдавливание, которое можно использовать для определения того, следует ли считать угол поворота положительным или отрицательным (см. Правило штопора ). Симметрии , показанные принадлежат к циклическим группам , чтобы и подгруппы соответствующих полных групп симметрии призм. Следует отметить, что эти трехмерные объекты обладают дополнительной вращательной и зеркальной симметрией. Представляя шесть показанных здесь правильных призм, все симметрии вращения однородного куба рассматриваются в следующем разделе . ${\ displaystyle C_ {1}}$${\ displaystyle C_ {6}}$

Вращательные симметрии куба

Все 13 осей вращательной симметрии однородного куба

Три 4-ходовые оси

Четыре 3-ходовые оси

Шесть двузначных осей

Однородный куб имеет в общей сложности 13 осей вращения (оси вращательной симметрии), как показано на рисунке ниже:

• 3 поверхности через центры противоположных сторон,
• 4 через противоположные углы и
• 6, которые проходят через центры противоположных краев.

Если посчитать элементы симметрии вращательной симметрии куба, то они следующие: нейтральный элемент , по 3 для 4-кратного, по 2 для 3-кратного и по одному для 2-кратных осей вращения. В общем, это элементы симметрии. ${\ Displaystyle 1 + 3 \ раз 3 + 4 \ раз 2 + 6 \ раз 1 = 24}$

Эти 24 элемента вместе образуют группу поворота куба . Куб и правильный октаэдр являются двойственными Платоновыми телами и имеют одинаковую симметрию. Таким образом, куб-токарной группы и октаэдр-токарной группы рассматриваются совместно в статье октаэдра группы . Если объединить группу вращения куба с точкой отражения в центре куба, получатся элементы полной группы симметрии куба ( см. Ниже ). ${\ Displaystyle 2 \ cdot 24 = 48}$

Зеркальная симметрия

Площадь Пьяцца дель Пополо с двумя (примерно) зеркально-симметричными церквями Санта-Мария-ди-Монте-Санто и Санта-Мария-деи-Мираколи (и Обелиско Фламинио )

Четыре зеркальные плоскости из девяти и одна из 13 осей вращения однородного куба

Зеркальная симметрия используется в двух значениях:

• Тело имеет зеркальную симметрию , если существует плоскость и отражение в этой плоскости является операцией симметрии рассматриваемого тела. Наблюдаемый объект конгруэнтен сам себе после отражения. Зеркало плоскость симметрии также просто называют зеркальной плоскости . В этом смысле зеркальная симметрия - автоморфизм . В математике автоморфизм - это отображение математического объекта на самого себя, при котором объект и отображаемый объект неотличимы.

• Два тела называются зеркально-симметричными друг другу, если они отличаются только отражением в одной плоскости. В просторечии говорят о зеркально перевернутой копии (или зеркально перевернутом изображении). Положение двух тел в космосе значения не имеет. Поэтому может потребоваться сначала переместить и повернуть, прежде чем будет найдена общая плоскость зеркала. Две церкви Санта-Мария-ди-Монте-Санто и Санта-Мария-деи-Мираколи на площади Пьяцца-дель-Пополо в Риме (приблизительно) зеркально-симметричны и обращены друг к другу, так что отражение возможно без смещения. Тогда церкви также будут зеркально-симметричными в первом значении термина, описанного выше. Еще один классический пример двух зеркально-симметричных зданий являются здания , известные как короля Карла суда и королевы Анны суда Королевского военно - морского колледжа в Гринвиче, построенный на Кристофера Рена .

Высокосимметричные объекты (например, некоторые из призм на рисунке напротив) могут иметь большое количество зеркальных плоскостей, которые пересекаются в одной точке. Сфера имеет бесконечное количество зеркальных плоскостей. На графике ниже справа показаны четыре из девяти зеркальных плоскостей и одна из 13 осей вращения однородного куба. Плоскости зеркала пересекаются по 4-кратной оси вращения. Симметрии показаны , имеют двугранной группу типа и является подгруппой в группе кубы . 48 элементов симметрии группы куба в целом делят куб на 48 (эквивалентных) фундаментальных областей . ${\ displaystyle D_ {4}}$

Вращающаяся зеркальная симметрия

Вращающаяся зеркальная симметрия - это симметрия тела, состоящая из двух подопераций. Первая подоперация - это вращение вокруг оси, оси вращающегося зеркала, вторая - зеркальное отображение на плоскости, перпендикулярной оси вращения, плоскости вращающегося зеркала. Эта плоскость проходит через центр симметрии, через центр тела. Если плоскость вращающегося зеркала не является плоскостью зеркальной симметрии тела, то обе подоперации не являются операциями симметрии сами по себе, а являются лишь их комбинацией. Последовательность частичных операций не важна. Мы также можем сначала выполнить зеркальное отображение, а затем вращение.

Вращающиеся зеркальные симметрии куба

Выбранные оси вращающегося зеркала и плоскости вращающегося зеркала однородного куба и эффект вращающегося зеркала

Одна из трех четырехходовых осей

Одна из четырех шестизначных осей

Одна из шести двукратных осей (инверсия)

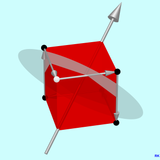
Вращения зеркальное отображение органов на себе является одним из менее известных, но , возможно, большинство операций симметрии интересно , что может быть легко поняты с помощью подходящих графики. На трех рисунках показан куб, одна из осей вращающегося зеркала и связанные с ними плоскости вращения зеркала. Чтобы отличить вращающиеся зеркальные плоскости от зеркальных плоскостей симметрии, они показаны серыми круглыми дисками, которые проекционно выглядят как эллипсы. Для графических кубов выбран полупрозрачный режим рисования . Поскольку оси вращающегося зеркала являются осями вращения, они будут расположены в порядке графика выше всех 13 осей вращательной симметрии ... расположенных.

На первом из трех рисунков показана одна из трех осей 4-кратного вращающегося зеркала и соответствующая плоскость вращающегося зеркала. Эффект поворотного зеркального отражения можно понять, проследив путь угла, отмеченного белой точкой. Плоскость вращающегося зеркала ориентирована через ось вращающегося зеркала. Таким образом, мы можем сказать, что белая точка находится над плоскостью вращающегося зеркала. После поворота на 90 ° (правило правой руки: большой палец в направлении оси, поворот в направлении других пальцев) точка сначала отображается в верхнем правом углу и, через отражение, в правом нижнем углу, который отмечен черной точкой. Точка и точка изображения соединены стрелкой. Новый поворот на 90 ° приводит к верхней правой черной точке и т. Д. После четырехкратного поворота снова достигается начальная точка.

Путь точки на кубе в общем положении представляет собой пространственный замкнутый зигзагообразный путь вокруг плоскости вращающегося зеркала. Если точка, по которой мы идем, лежит в плоскости вращающегося зеркала, ее путь будет квадратным. Если он лежит на оси вращающегося зеркала, он четыре раза прыгает вперед и назад по оси вращающегося зеркала, отражаясь плоскостью вращающегося зеркала. Центр симметрии, центр тяжести куба всегда отображается сам на себя. Обратите внимание, что вращающаяся зеркальная плоскость в этом случае также является зеркальной плоскостью симметрии куба.

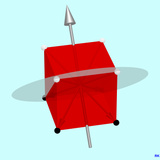
Интересен случай одной из четырех осей 6-кратного вращающегося зеркала, показанных на втором рисунке. Интересно с одной стороны, потому что плоскость вращающегося зеркала, очевидно, не является плоскостью зеркальной симметрии куба. С другой стороны, потому что ось 3-кратного вращения становится осью зеркала 6-кратного вращения. Вы можете увидеть, что он состоит из 6 цифр, если проследите путь, за которым следует точка на кубе, например, на графике путь угла, отмеченного белой точкой. С помощью первой подоперации, поворота на 60 ° вокруг оси вращающегося зеркала, белая точка сопоставляется с точкой, которая не является угловой. Вторая подоперация, зеркальное отображение на плоскости вращающегося зеркала, приводит к первой точке изображения, которая отмечена как черная точка и находится над плоскостью вращающегося зеркала (черная точка вверху справа). Опять же, точка и точка изображения соединены стрелкой. Если вы теперь снова примените поворотное зеркальное отображение на 60 ° к первой точке изображения, это приведет ко второй черной точке изображения в правом нижнем углу и т. Д. После 6 поворотных зеркальных отражений на 60 ° каждое снова будет достигнута белая начальная точка. Если точка, которую мы отслеживаем, лежит в плоскости вращающегося зеркала, ее путь представляет собой правильный шестиугольник .

Вероятно, неожиданным является эффект 2-кратного зеркального отражения, которому посвящен третий рисунок. Показана одна из осей 2-кратного вращающегося зеркала, которых мы ожидаем шесть, исходя из аналогии с вращающимися осями. Если мы выполним двукратное вращающееся зеркальное отображение в соответствии с процедурой, описанной выше, мы обнаружим, что каждая точка куба отображается на свой « антипод », то есть в точку на противоположной стороне куба. Точка и точка изображения лежат вместе с центром симметрии на прямой и находятся на одинаковом расстоянии от центра симметрии. В этом случае на графике отмечены четыре белые точки, а их пиксели отмечены как четыре черных. Все четыре вектора связи между точкой и точкой изображения пересекаются в центре симметрии.

Также интересен тот факт, что вращающиеся зеркальные изображения вокруг всех шести возможных двукратно вращающихся осей зеркала приводят к одному и тому же типу симметрии. Этот тип симметрии, точечное отражение в центре симметрии, называется инверсией в теории групп и кристаллографии . Поэтому из соображений симметрии можно опустить все оси 2-кратного вращающегося зеркала и заменить их одной операцией - инверсией.

Поворотное зеркальное отображение не оставляет точки на кубе, то есть угла, но также не оставляет поверхности или края на их исходном месте. Единственная фиксированная точка вращательного зеркального отражения - это центр симметрии, центр куба, на который уже указывалось.

Одна из трех осей четырехкратного вращающегося зеркала с вращающейся зеркальной плоскостью однородного правильного тетраэдра.

Однородный правильный тетраэдр также имеет четырехкратную вращающуюся зеркальную симметрию однородного куба, как показано на рисунке с использованием оси в качестве примера. Как видно из рисунка, в отличие от куба, плоскость вращающегося зеркала не является плоскостью зеркальной симметрии тетраэдра. Каркасная модель охватывающего куба также нарисована на графике.

Различия между зеркальным отображением вращения и вращением

Свойства вращающихся отражений отличаются от свойств вращений:

• Оси вращения тела также могут быть осями вращающегося зеркала тела, но не каждая ось вращения обязательно является осью вращающегося зеркала. В случае тетраэдра, например, его 3-кратные оси вращения не являются осями вращения зеркала.
• Произведение операции симметрии вращения с самим собой всегда является новым элементом симметрии группы. При n-кратной оси вращения мощность увеличивается до (n-1). Результатом операции симметрии вращающейся оси зеркала с самим собой является не новый элемент симметрии группы, а (одиночное) вращение в результате двойного зеркального отражения.
• Счетчики оси вращения и оси выпрямленного вращающегося зеркала могут быть одинаковыми (оба 4-значные на первом графике для куба) или могут быть разными (3-значные для симметрии вращения и 6-значные для вращающегося зеркала. симметрия на втором рисунке).
• Каждая вращающаяся зеркальная ось куба имеет два элемента симметрии на каждую вращающуюся зеркальную ось, независимо от их количества. Поскольку куб имеет три 4-значных и четыре 3-значных оси вращающихся зеркал, существуют вращающиеся зеркальные элементы группы куба в более узком смысле. Кроме того, существует точка зеркального отображения всех 2-кратно вращающиеся оси зеркал, инверсия, так что в общей сложности 15 вращающихся зеркальных элементов приводят.${\ Displaystyle 2 \ cdot (3 + 4) = 14}$

Как упоминалось в начале, отражение точки в двухмерных терминах синонимично повороту на 180 ° вокруг фиксированной точки и, следовательно, отсутствию отдельного элемента симметрии.

Точечная симметрия / инверсионная симметрия

Эффект точечного отражения / инверсии для четырех выбранных углов куба

Как описано в предыдущем разделе, точечная симметрия или инверсионная симметрия - это симметрия тела относительно точки, центра симметрии. Каждая точка меняет свое положение с точкой, которая находится на прямой линии, идущей от этой точки через центр и лежащей по другую сторону от центра на том же расстоянии. Это точечное отражение тела на самом себе.Точечное отражение не оставляет никакой точки тела на исходном месте, за одним исключением: единственная фиксированная точка отражения вращения - это центр симметрии, центр тела.

На графике показано отображение четырех выбранных углов (белые точки) куба путем инверсии (черные точки). И наоборот, все черные точки отображаются на белые. Рисунок является повторением третьего рисунка выше ( выбранные оси вращающегося зеркала ... ) без двукратной оси вращения зеркала и вращающейся плоскости зеркала.

Однородные Платоновы тела - куб , октаэдр , додекаэдр и икосаэдр - точечно-симметричны. Напротив, простейшее платоново твердое тело, правильный тетраэдр , таковым не является.

В случае куба (включая инверсию) было 15 вращающихся зеркальных симметрий. Вместе с 9 зеркальными уровнями это дает 24 элемента симметрии, то есть ровно столько, сколько элементов вращающейся группы куба. Это не случайно, потому что каждое зеркало или вращающийся зеркальный элемент можно интерпретировать как комбинацию вращения и инверсии. В этом смысле инверсия обратно симметричного тела занимает такое же важное место, как и нейтральный элемент в группе симметрии.

Сферическая симметрия

Вращательная симметрия относительно любой оси, проходящей через одну и ту же точку, является частным случаем вращательной симметрии и называется сферической или радиальной симметрией. Звезды - это z. Б. примерно сферически симметричны, так как их свойства (например, плотность) не везде одинаковы, а зависят только от расстояния до центра. Их гравитационные поля, а также z. Б. электрическое поле заряженной сферы сферически симметрично.

Комбинации

Симметричные базовые операции могут быть получены из возможности комбинирования операций симметрии:

1. Идентичность (нулевая операция, без изменений)
2. Вращение ( вращение )
3. Rotation - Inversion ( зеркальное отображение вращения )
4. Перевод (смещение)
5. Скользящее отражение
6. Завинчивание

Смотри тоже

• Симметрия (физика)
• Группа симметрии

литература

• Герман Вейль : Симметрия: Дополнен текстом «Симметрия и конгруэнтность» из поместья и комментариями Доменико Джулини, Эрхарда Шольца и Клауса Фолькерта. Переводчик Лулу Хофманн Бехтольшайм . 3. Издание. Springer Spectrum, Berlin, Heidelberg 2017, ISBN 978-3-662-52711-5 (VII, 232, ограниченный предварительный просмотр в поиске книг Google [доступ 23 июля 2019 г.]).  Перепечатка оригинала 1952 года в Hermann Weyl: Symmetry . Princeton University Press, Princeton, NJ 2015 (176 стр., Ограниченный предварительный просмотр в Поиске книг Google [доступ 23 июля 2019 г.]). 
• Х. Шупп: Элементарная геометрия . UTB Schöningh 1977, ISBN 3-506-99189-2 , стр. 35, 45.
• Уилл Клебер и др. : Введение в кристаллографию . 19-е, улучшенное издание. Oldenburg Verlag, Мюнхен 2010, ISBN 978-3-486-59075-3 (470 страниц, ограниченный предварительный просмотр в поиске книг Google [доступ 18 августа 2019 г.]). 
• Вернер Хан: Симметрия как принцип развития в природе и искусстве . С предисловием Руперта Ридла. Кенигштейн я. Ц. ( издательство Langewiesche ) 1989.
• М. И. Войцеховский: Симметрия . В: Michiel Hazewinkel (Ed.): Encyclopedia of Mathematics . Springer-Verlag и EMS Press, Берлин 2002, ISBN 978-1-55608-010-4 (английский, онлайн ). 
• Артур Шенфлис: Кристаллические системы и кристаллическая структура . Teubner, Leipzig 1891 (XII, 638 с., Интернет-ресурсы ). 
• Дэвид Уэйд: Сила симметрии. Artemis & Winkler Verlag 2011, ISBN 978-3-538-07311-1

веб ссылки

Викисловарь: Симметрия  - объяснение значений, происхождение слов, синонимы, переводы

Индивидуальные доказательства

1. ↑ Терминология не всегда последовательна. Вращательная симметрия вокруг фиксированного угла также называется вращательной симметрией , чтобы отличать ее от вращательной симметрии , например, окружности.
2. ↑ Клебер 2010, с. 52
3. ↑ вращательная симметрия. Проверено 20 ноября 2019 года . 
4. ↑ ^{a b} Большой карманный словарь Мейера в 24 томах . BI-Taschenbuchverlag 1992, Том 21, с. 258.
5. ↑ Введение в Материаловедения I. извлекаться 26 сентября 2020 . 
6. ↑ зеркальная плоскость в: Ричард Рулевой (ред.): Физика: Том 2 / Ma-Z . 2-е издание. Brockhaus, Лейпциг 1989, ISBN 3-325-00192-0 , стр.  909 (страницы 601-1146, 48 табличек). 
7. ↑ Очевидный термин « автомобильная зеркальная симметрия», который отличал бы эту зеркальную симметрию от зеркальной симметрии в первом значении, не является распространенным (в Google не попал).
8. ↑ Клебер 2010, стр. 60 и сл.
9. ↑ Обратите внимание, что инверсия имени также используется для отражения на круге .
10. ↑ Шенфлис указывает на странице 90 своей монографии, что следует опустить оси двойной зеркальной симметрии , которые он называет осями двойной симметрии второго рода , и говорить только об инверсии: «Операция, которая характерна для оси двойной симметрии второй вид - инверсия. Таким образом, ось представляет то же свойство симметрии, что и центр симметрии. Но для центра симметрии больше нет особого направления; ему эквивалентна каждая двукратная ось второго рода. По этой причине желательно полностью оставить топоры второго типа вне игры; В противном случае легко могло бы возникнуть ошибочное мнение, что и для них направление, представленное осью, имеет особое значение для соответствующего свойства симметрии ".