Пирамида (геометрия)

Пирамиды является геометрическое тело , точнее многогранник , основание которого представляет собой многоугольник , и чьи боковые поверхности являются треугольники , которые, с одной стороны , являются смежными с полигона , а с другой стороны , встречаются в точке, так называемый наконечник пирамида. Многоугольник еще называют основанием пирамиды. Треугольники вместе образуют внешнюю поверхность пирамиды.

строительство

С отличной точки , вершины пирамиды, опирается пучок лучей, излучение которых представляет собой плоскость, прорезанную по углам основания пирамиды. Используя четыре луча с определенным наклоном в пространстве, вы, например, получите квадратное основание и, таким образом, образуете квадратную пирамиду. Вы также можете начать построение с любой базовой области многоугольника плоскости и выбрать точку за пределами этой плоскости, которая затем станет вершиной пирамиды. Соединяя каждый угол основания с кончиком, создается вышеупомянутый пучок лучей. Точки каждого отдельного ребра основания соединены с вершиной пирамиды через треугольную поверхность. Таким образом , пирамида также выполняет определение в конусах .

характеристики

Если у основания пирамиды есть углы , то количество треугольных боковых поверхностей также одинаково, а вместе с основанием пирамида имеет общее количество поверхностей . Количество углов также , а именно углы в основании плюс наконечника. Основание содержит ребра. Вместе с таким же количеством боковых линий пучка лучей, соединяющих углы основания с вершиной пирамиды, пирамида в целом имеет ребра. В случае пирамиды этот подсчет подтверждает замену многогранника Эйлера через количество углов, количество ребер и количество граней многогранника: ${\ displaystyle n}$ ${\ displaystyle n.}$${\ displaystyle n + 1}$ ${\ displaystyle n + 1,}$${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle 2 \ cdot n}$${\ displaystyle E}$${\ displaystyle K}$${\ displaystyle F}$

${\ Displaystyle Е-К + F = (п + 1) -2 \ CDOT п + (п + 1) = 2}$

Понятие высоты пирамиды важно для расчета объема . Под этим понимается расстояние между вершиной пирамиды и плоскостью, в которой находится основание.

Центр тяжести пирамиды лежит на соединительную линии между центром тяжести основания и вершиной пирамиды. Он делит это расстояние в соотношении 1: 3 и, следовательно, имеет расстояние от базовой плоскости. ${\ displaystyle {\ tfrac {h} {4}}}$

Правильная пирамида

Пирамида, основание которой представляет собой равносторонний треугольник, а три боковые поверхности - треугольники, конгруэнтные основанию, называется правильным тетраэдром .

Пирамида, основание которой представляет собой квадрат, а вершина пирамиды перпендикулярна центру основания, называется квадратной пирамидой.

Тетраэдр и квадратные пирамиды , так называемые регулярные или регулярные пирамиды. Один говорит на регулярной или регулярной пирамиды , когда основание пирамиды является правильный многоугольник , и центром этого многоугольника также основание высоты пирамиды. Тогда другие боковые грани представляют собой равнобедренные треугольники . Следовательно, любая правильная пирамида также является прямой (см. Раздел Прямая пирамида ).

Обычная пирамида полностью определяется тремя определяющими частями, например, если даны количество углов / краев области основания, длина стороны области основания и высота .

• 

  Тетраэдр

• 

  Квадратная пирамида

• 

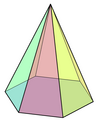
  Правильная пятигранная пирамида

• 

  Обычная шестигранная пирамида

Прямая пирамида

Прямая пирамида

Если вершина пирамиды расположена над ее основанием таким образом, что силуэт кажется наблюдателю, находящемуся в плоскости основания, как равнобедренный треугольник со всех возможных направлений , то он называется прямым.

Если основание осесимметрично , то в случае прямых пирамид отвес совпадает с центром симметрии и центром тяжести основания. Если основание не только осесимметрично, но и является правильным многоугольником , то все боковые грани, т.е. ЧАС. все края, начинающиеся от кончика, одинаковой длины.

В случае прямой пирамиды с квадратом дракона в качестве основания базовая точка находится в середине диагоналей , которая является осью симметрии, а не на пересечении диагоналей или в центре тяжести .

Основание пирамиды не имеет симметрии на, то этот термин имеет только не разумный смысл больше: Если базовая область, например, любой треугольник , так должно вершина пирамиды вертикально над его окружности лежат, таким образом , что все боковые ребра равной длины. Если этот треугольник имеет тупой угол , то отвес наконечника даже лежит за пределами области основания, что противоречит иллюстративному значению прямого .

Наклонная пирамида

Наклонная пирамида

Пирамида с правильным многоугольником в качестве основания называется наклонной, если не все боковые стороны имеют одинаковую длину, основание перпендикуляра от вершины не находится в центре основания и, следовательно, соединительная линия от и не перпендикулярна основание пирамиды. В случае изогнутой пирамиды точка основания перпендикуляра от вершины может быть расположена как внутри, так и снаружи основания пирамиды. ${\ displaystyle S}$ ${\ displaystyle M}$${\ displaystyle M}$${\ displaystyle S}$${\ displaystyle S}$

Тела Джонсона J ₁ и J ₂

Квадратная пирамида, четыре треугольные стороны которой равносторонние, - это простейшее поле Джонсона , сокращенно J ₁ . Правильная пятигранная пирамида, пять треугольных сторон которой равносторонние, и есть поле Джонсона J ₂ .

Формулы общей пирамиды

объем

Объем пирамиды рассчитывается исходя из площади основания и высоты в соответствии с ${\ displaystyle V}$${\ displaystyle G}$${\ displaystyle h}$

${\ Displaystyle V = {\ гидроразрыва {1} {3}} \ cdot G \ cdot h}$

Эта формула применима к любой пирамиде. Так что не имеет значения, является ли основание треугольником, квадратом, пятиугольником ... - оно также может быть круглым или деформированным. Формула также действительна, если базовая точка высоты не совпадает с центральной точкой базовой области или базовая область вообще не имеет центральной точки; базовая точка высоты может также находиться за пределами базовой области.

Общая формула также соответствует формуле объема для кругового конуса . Под конусом также понимается пирамида с правильным углом в качестве основания, которая после пересечения границы превратилась в круг. ${\ Displaystyle V = {\ гидроразрыва {1} {3}} \ cdot G \ cdot h}$${\ Displaystyle V = {\ гидроразрыва {1} {3}} \ cdot (\ pi \ cdot r ^ {2}) \ cdot h}$${\ displaystyle n}$${\ Displaystyle п \ к \ infty}$

Поверхность и боковая поверхность

Поверхность пирамиды состоит из основания и внешней поверхности.${\ displaystyle O}$${\ displaystyle G}$${\ Displaystyle M \ двоеточие}$

${\ displaystyle O = G + M}$

Формулы для правильных пирамид

Размеры правильной пирамиды высотой h и правильного угла n с длиной стороны a в качестве основания
	Общий случай	Квадратная пирамида	Правильная треугольная пирамида
объем	${\ displaystyle V = {\ frac {n \ cdot a ^ {2} \ cdot h} {12}} \ cdot \ cot \ left ({\ frac {\ pi} {n}} \ right)}$	${\ Displaystyle V = {\ гидроразрыва {а ^ {2} \ cdot h} {3}}}$	${\ Displaystyle В = {\ гидроразрыва {а ^ {2} \ cdot h} {12}} \ cdot {\ sqrt {3}}}$
поверхность	${\ displaystyle O = {\ frac {n \ cdot a} {4}} \ cdot \ left (a \ cdot \ cot \ left ({\ frac {\ pi} {n}} \ right) + {\ sqrt { 4 \ cdot h ^ {2} + a ^ {2} \ cdot \ cot ^ {2} \ left ({\ frac {\ pi} {n}} \ right)}} \ right)}$	${\ displaystyle O = a ^ {2} + a \ cdot {\ sqrt {4 \ cdot h ^ {2} + a ^ {2}}}}$	${\ displaystyle O = {\ frac {3 \ cdot a} {4}} \ cdot \ left ({\ frac {a} {3}} \ cdot {\ sqrt {3}} + {\ sqrt {4 \ cdot) h ^ {2} + {\ frac {a ^ {2}} {3}}}} \ right)}$
Длина крутого края	${\ displaystyle l = \ left (h ^ {2} + {\ frac {a ^ {2}} {4 \ cdot \ sin ^ {2} \ left ({\ frac {\ pi} {n}} \ right) )}} \ right) ^ {\ frac {1} {2}}}$	${\ displaystyle l = {\ sqrt {h ^ {2} + {\ frac {a ^ {2}} {2}}}}}$	${\ displaystyle l = {\ sqrt {h ^ {2} + {\ frac {a ^ {2}} {3}}}}}$
Умкугельрадиус	${\ displaystyle r_ {u} = {\ frac {h} {2}} + {\ frac {a ^ {2}} {8 \ cdot h \ cdot \ sin ^ {2} \ left ({\ frac {\ pi} {n}} \ right)}}}$	${\ displaystyle r_ {u} = {\ frac {h} {2}} + {\ frac {a ^ {2}} {4 \ cdot h}}}$	${\ displaystyle r_ {u} = {\ frac {h} {2}} + {\ frac {a ^ {2}} {6 \ cdot h}}}$
Inc радиус сферы	${\ displaystyle r_ {i} = {\ frac {a \ cdot h} {a + {\ sqrt {4 \ cdot h ^ {2} \ cdot \ tan ^ {2} \ left ({\ frac {\ pi}) {n}} \ right) + a ^ {2}}}}}}$	${\ displaystyle r_ {i} = {\ frac {a \ cdot h} {a + {\ sqrt {4 \ cdot h ^ {2} + a ^ {2}}}}}}$	${\ displaystyle r_ {i} = {\ frac {a \ cdot h} {a + {\ sqrt {12 \ cdot h ^ {2} + a ^ {2}}}}}}$
Угол основания равнобедренных треугольников	${\ displaystyle \ alpha _ {1} = \ alpha _ {2} = \ arctan \ left ({\ frac {1} {a}} \ cdot {\ sqrt {4 \ cdot h ^ {2} + a ^ { 2} \ cdot \ cot ^ {2} \ left ({\ frac {\ pi} {n}} \ right)}} \ right)}$	${\ displaystyle \ alpha _ {1} = \ alpha _ {2} = \ arctan \ left ({\ frac {1} {a}} \ cdot {\ sqrt {4 \ cdot h ^ {2} + a ^ { 2}}} \ right)}$	${\ displaystyle \ alpha _ {1} = \ alpha _ {2} = \ arctan \ left ({\ frac {1} {a}} \ cdot {\ sqrt {4 \ cdot h ^ {2} + {\ frac {a ^ {2}} {3}}}} \ right)}$
Угол вверху равнобедренных треугольников	${\ displaystyle \ alpha _ {3} = 2 \ cdot \ arctan \ left ({\ frac {a} {\ sqrt {4 \ cdot h ^ {2} + a ^ {2} \ cdot \ cot ^ {2}) \ left ({\ frac {\ pi} {n}} \ right)}}} \ right)}$	${\ displaystyle \ alpha _ {3} = 2 \ cdot \ arctan \ left ({\ frac {a} {\ sqrt {4 \ cdot h ^ {2} + a ^ {2}}}} \ right)}$	${\ displaystyle \ alpha _ {3} = 2 \ cdot \ arctan \ left ({\ frac {a} {\ sqrt {4 \ cdot h ^ {2} + {\ frac {a ^ {2}} {3}) }}}} \ Правильно)}$
Угол между основанием и равнобедренным треугольником	${\ displaystyle \ beta _ {1} = \ arctan \ left ({\ frac {2 \ cdot h \ cdot \ tan \ left ({\ frac {\ pi} {n}} \ right)} {a}} \ Правильно)}$	${\ displaystyle \ beta _ {1} = \ arctan \ left ({\ frac {2 \ cdot h} {a}} \ right)}$	${\ displaystyle \ beta _ {1} = \ arctan \ left ({\ frac {2 \ cdot {\ sqrt {3}} \ cdot h} {a}} \ right)}$
Угол между равнобедренными треугольниками	${\ displaystyle \ beta _ {2} = 2 \ cdot \ arctan \ left ({\ frac {1} {2 \ cdot h}} \ cdot \ left ({\ frac {4 \ cdot h ^ {2} \ cdot) \ sin ^ {2} \ left ({\ frac {\ pi} {n}} \ right) + a ^ {2}} {\ tan ^ {2} \ left ({\ frac {\ pi} {n} } \ right) - \ sin ^ {2} \ left ({\ frac {\ pi} {n}} \ right)}} \ right) ^ {\ frac {1} {2}} \ right)}$	${\ displaystyle \ beta _ {2} = 2 \ cdot \ arctan \ left ({\ frac {1} {2 \ cdot h}} \ cdot {\ sqrt {4 \ cdot h ^ {2} +2 \ cdot a ^ {2}}} \ right)}$	${\ displaystyle \ beta _ {2} = 2 \ cdot \ arctan \ left ({\ frac {1} {3 \ cdot h}} \ cdot {\ sqrt {3 \ cdot h ^ {2} + a ^ {2) }}} \ Правильно)}$
Телесный уголок на основании	${\ displaystyle \ Omega _ {1} = 4 \ cdot \ arctan \ left ({\ sqrt {\ tan \ left ({\ frac {2 \ cdot \ beta _ {1} + \ beta _ {2}} {4) }} \ right) \ cdot \ tan \ left ({\ frac {2 \ cdot \ beta _ {1} - \ beta _ {2}} {4}} \ right) \ cdot \ tan ^ {2} \ left ({\ frac {\ beta _ {2}} {4}} \ right)}} \ right)}$
Телесный угол вверху	${\ displaystyle \ Omega _ {2} = 2 \ cdot \ pi -2 \ cdot n \ cdot \ arcsin \ left (\ cos \ left ({\ frac {\ pi} {n}} \ right) \ cdot {\ sqrt {\ tan ^ {2} \ left ({\ frac {\ pi} {n}} \ right) - \ tan ^ {2} \ left ({\ frac {\ alpha _ {3}} {2}} \ верно-верно)}$

Особые случаи

Для определенных значений и существуют отношения с платоновыми телами : ${\ displaystyle n}$${\ displaystyle h}$

• Для и получаем правильный тетраэдр .${\ displaystyle n = 3}$${\ displaystyle h = {\ frac {a} {3}} \ cdot {\ sqrt {6}}}$
• Для и результата является квадратной пирамидой , которая является половиной октаэдр .${\ displaystyle n = 4}$${\ displaystyle h = {\ frac {a} {2}} \ cdot {\ sqrt {2}}}$
• Ибо есть правильная пятигранная пирамида, которая является частью икосаэдра .${\ displaystyle n = 5}$${\ displaystyle h = {\ frac {a} {10}} \ cdot {\ sqrt {50-10 \ cdot {\ sqrt {5}}}}}$

Соединение с круговым конусом

Правильные пирамиды, которые имеют правильный многоугольник в качестве основания, могут использоваться для аппроксимации кругового конуса , который по определению имеет круг в качестве основания.

Если у правильного многоугольника есть углы , т.е. это угол, то можно формально сформировать предельное значение для бесконечно большого размера . Круговой конус можно понимать как правильную пирамиду, так сказать, с площадью основания, имеющей бесконечное количество углов, и длиной стороны угла, имеющей предельное значение 0. ${\ displaystyle n}$ ${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle n}$

В последующем, объем в круговом конусе должны быть получен таким образом .

С помощью формулы для области регулярного угла (см правильного многоугольника - периметр и площадь ) следующие результаты для объема обычной пирамиды, если радиус из по периметру в углу , как известен: ${\ displaystyle n}$${\ displaystyle V}$ ${\ displaystyle r_ {u}}$${\ displaystyle n}$

${\ displaystyle V = {\ frac {A \ cdot h} {3}} = {\ frac {n \ cdot r_ {u} ^ {2} \ cdot h} {3}} \ cdot \ sin \ left ({ \ frac {2 \ pi} {n}} \ right)}$

Для того , чтобы определить объем кругового конуса , то предельное значение для к бесконечности может быть сформировано. Это предельное значение получается следующим образом (см. Правильный многоугольник - сходимость с заданным радиусом ): ${\ displaystyle n}$

${\ Displaystyle V _ {\ mathrm {круговой конус}} = \ lim _ {n \ to \ infty} {\ frac {A \ cdot h} {3}} = \ lim _ {n \ to \ infty} {\ frac {n \, r_ {u} ^ {2}} {2}} \ cdot \ sin \ left ({\ frac {2 \ pi} {n}} \ right) = {\ frac {\ pi \ cdot r_ {u} ^ {2} \ cdot h} {3}}}$

Среди прочего, формула для объема получается, когда длина стороны области основания известна с помощью уравнений для правильного угла. ${\ displaystyle V = {\ frac {n \ cdot a ^ {2} \ cdot h} {12}} \ cdot \ cot \ left ({\ frac {\ pi} {n}} \ right)}$${\ displaystyle a}$ ${\ displaystyle n}$

Пример расчета на квадратной пирамиде

Боковая поверхность и поверхность

Поверхность квадратной пирамиды как сеть тел

Симметричная сетка тела квадратной пирамиды (альтернативное представление сетки)

Поверхность квадратной пирамиды состоит из квадратного основания и внешней поверхности.${\ displaystyle G}$${\ displaystyle M.}$

Если указать длину стороны квадрата, мы получим, потому что${\ displaystyle a}$${\ displaystyle G = a ^ {2} \ двоеточие}$

${\ displaystyle O = a ^ {2} + M}$

В случае правильной пирамиды с квадратным основанием, внешняя поверхность состоит из четырех поверхностей конгруэнтных равнобедренных треугольников .

Пусть заданы длина стороны и высота пирамиды : ${\ displaystyle a}$${\ displaystyle h}$

Площадь одного из этих треугольников равна площади всех четырех областей . Вот высота совпадающих боковых треугольников. ${\ displaystyle A_ {D} = {\ frac {a \ cdot h_ {a}} {2}}}$${\ Displaystyle М = 2 \ cdot а \ cdot h_ {а}}$${\ displaystyle h_ {a}}$

Это следует из теоремы Пифагора . Отсюда и для боковой поверхности следует${\ Displaystyle {ч_ {а}} ^ {2} = ч ^ {2} + ({\ tfrac {а} {2}}) ^ {2}}$${\ displaystyle h_ {a} = {\ sqrt {h ^ {2} + ({\ tfrac {a} {2}}) ^ {2}}}}$${\ displaystyle M = a \ cdot {\ sqrt {4 \ cdot h ^ {2} + a ^ {2}}}.}$

Таким образом, общая поверхность ${\ displaystyle O = a ^ {2} + a \ cdot {\ sqrt {4 \ h ^ {2} + a ^ {2}}}.}$

Длина крутого края

В дополнение к четырем краям основания квадратная пирамида имеет четыре крутых края равной длины (также называемые гребнями) , которые начинаются от угловых точек основания и поднимаются вверх и встречаются на вершине пирамиды . ${\ displaystyle a}$${\ Displaystyle AS, BS, CS}$${\ displaystyle DS,}$${\ displaystyle S}$

Пусть заданы длина стороны и высота пирамиды : ${\ displaystyle a}$${\ displaystyle h}$

Теорема Пифагора дает длину диагонали основания , из которой она следует. ${\ displaystyle d}$${\ displaystyle d ^ {2} = a ^ {2} + a ^ {2},}$${\ displaystyle d = a \ cdot {\ sqrt {2}}}$

Для дальнейшего расчета необходимо, а его квадрат равен${\ displaystyle {\ tfrac {d} {2}} = {\ tfrac {a} {2}} \ cdot {\ sqrt {2}}}$${\ displaystyle {\ tfrac {a ^ {2}} {2}}.}$

Для вычисления одного снова используется теорема Пифагора: и это следует для гребня${\ Displaystyle AS}$${\ displaystyle {AS} ^ {2} = h ^ {2} + {\ tfrac {a ^ {2}} {2}}}$${\ displaystyle AS = {\ sqrt {h ^ {2} + {\ tfrac {a ^ {2}} {2}}}}.}$

Общая длина кромки

Общая длина ребра квадратной пирамиды состоит из четырех сторон и четырех равных по длине ребер и . Опять же, пусть заданы длина стороны и высота пирамиды : ${\ displaystyle K}$${\ displaystyle a}$${\ Displaystyle AS, BS, CS}$${\ displaystyle DS}$${\ displaystyle a}$${\ displaystyle h}$

${\ Displaystyle К = 4 \ cdot a + 4 \ cdot {\ sqrt {h ^ {2} + {\ frac {a ^ {2}} {2}}}}}$

${\ displaystyle K = 4 \ cdot \ left (a + {\ sqrt {h ^ {2} + {\ frac {a ^ {2}} {2}}}} \ right)}$

Объем как крайнее значение

Бумажная модель квадратной пирамиды с максимальным объемом для заданной площади поверхности

Квадратная пирамида с максимальным объемом является сравнительно остроконечной: из всех квадратных пирамид с одинаковой поверхностью та, которая является высокой, имеет наибольший объем (если длина ее основания указывает размер). Его объем такой , треугольники его боковой поверхности высокие. ${\ Displaystyle ч = а \ cdot {\ sqrt {2}}}$${\ displaystyle a}$${\ displaystyle V = {\ frac {1} {3}} \ cdot a ^ {3} \ cdot {\ sqrt {2}}}$${\ displaystyle {\ frac {3} {2}} \ cdot a}$

Вывод формулы объема для общей пирамиды

Есть несколько способов получить объем общей пирамиды:

Расчет с использованием позднего продукта

Трехсторонняя пирамида, натянутая на векторы, имеет объем ${\ displaystyle {\ vec {a}}, {\ vec {b}}, {\ vec {c}}}$

${\ displaystyle V = {\ frac {1} {6}} \ cdot | ({\ vec {a}} \ times {\ vec {b}}) \ cdot {\ vec {c}} |.}$

Элементарное геометрическое обоснование

Вышеупомянутую формулу объема можно обосновать двумя основными шагами:

1. Куб можно разделить на три равные пирамиды с квадратным основанием, вершины которых совпадают в одном углу куба. Три базовые поверхности - это три боковые поверхности куба, которые не содержат эту общую точку.
2. Две пирамиды с одинаковым основанием и одинаковой высотой имеют одинаковый объем.

Чтобы доказать это утверждение, можно использовать принцип Кавальери и законы центрического удлинения .

Таким образом, формула объема применима к пирамидам. ${\ displaystyle V = {\ frac {1} {3}} \ cdot G \ cdot h.}$

Обоснование с помощью интегрального исчисления

Объем пирамиды с основанием и высотой можно вычислить, если представить пирамиду состоящей из тонких ( бесконечно малых ) слоев толщины, параллельных основанию. Ось теперь находится через вершину пирамиды , так что высота совпадает с осью. Если обозначить площадь слоя на расстоянии от острия , можно вывести формулу из законов центрического растяжения : ${\ displaystyle G}$${\ displaystyle h}$${\ displaystyle \ mathrm {d} y}$${\ displaystyle y}$${\ displaystyle h}$${\ displaystyle y}$${\ displaystyle y}$${\ Displaystyle А (у)}$${\ Displaystyle А (у)}$

${\ displaystyle A (y): G = y ^ {2}: h ^ {2}}$

${\ Displaystyle А (у) = {\ гидроразрыва {G} {ч ^ {2}}} у ^ {2}}$

Это приводит к объему пирамиды путем интеграции в вверх к принципу Кавальери : ${\ displaystyle y = 0}$${\ displaystyle y = h}$

${\ Displaystyle V = \ int _ {0} ^ {h} A (y) \, \ mathrm {d} y = \ int _ {0} ^ {h} {\ frac {G} {h ^ {2} }} y ^ {2} \, \ mathrm {d} y = {\ frac {G} {h ^ {2}}} \ int _ {0} ^ {h} y ^ {2} \, \ mathrm { d} y = {\ frac {G} {h ^ {2}}} \ cdot {\ frac {1} {3}} \ left [y ^ {3} \ right] _ {0} ^ {h} = {\ frac {G} {h ^ {2}}} \ cdot {\ frac {1} {3}} \ left [h ^ {3} -0 \ right] = {\ frac {1} {3}} G \ cdot h}$

Измерение пирамидальной конструкции

Просмотр на расстоянии и определение угла обзора в упрощенном виде

С большой пирамидой можно напрямую измерить длину краев основания, но не высоту, которая напрямую недоступна. Далее будут представлены фундаментальные трудности, которые не столько связаны с методологией самого процесса измерения. Простым геометрическим методом определения высоты более крупных объектов является наблюдение с расстояния и определение угла обзора (в упрощенном виде показано на соседнем рисунке).

На расстоянии от нижнего края пирамиды вершина пирамиды визируется под измеренным углом . Таким образом, расстояние между точкой наблюдения и вершиной пирамиды на горизонтальной линии составляет половину стороны основания. Высота определяется формулой на графике. Определить высоту не составит большого труда. Однако есть следующие сложности: ${\ displaystyle s}$${\ displaystyle \ alpha}$${\ displaystyle a / 2 + s.}$${\ displaystyle h}$

• Вершина пирамиды не обязательно находится точно над центром основания.
• Длину основания пирамиды точно определить невозможно (битые камни, эрозия).
• Наконечника больше нет (износился).
• Угол наклона пирамиды определить сложно (эрозия, эрозия).

Это во многом соответствует реальности известных великих пирамид. Необходимо точно учитывать отклонение по высоте точки наблюдения, в которой производятся измерения. Само измерение угла обычно может быть выполнено очень точно. Кроме того, необходимо определить, с какого уровня земли должна быть допустима высота пирамиды, т. Е. Где она должна начинаться. Предположим, что базовая длина пирамиды не может быть определена более точно, чем 30 см, и поэтому расстояние до точки измерения не может быть определено более точно, чем 15 см. В результате при предполагаемом угле обзора 35 ° высота будет неточной примерно на 10 см. Чего сейчас не хватает, так это определения угла наклона боковой поверхности. Гипотетическая большая пирамида с базовой длиной 200 м и высотой 140 м будет иметь погрешность угла наклона около одной угловой минуты (54 ° 27'44 « по сравнению с 54 ° 26'34» с неточностью из информация о высоте 10 см ). Теперь это относится к пирамидам, вершина которых все еще на месте. На самом деле все иначе. Определение высоты отражает не исходную высоту, а высоту удаленной пирамиды. ${\ displaystyle \ alpha}$${\ displaystyle a}$${\ displaystyle a / 2 + s}$${\ displaystyle \ alpha}$${\ displaystyle \ beta}$${\ displaystyle h = 140 {,} 0 \, \ mathrm {m}}$${\ displaystyle h = 139 {,} 9 \, \ mathrm {m}}$

Проблема с экстраполяцией

Таким образом, пик необходимо экстраполировать . На картинке справа схематично показана проблема. И боковые поверхности, и наконечник явно изношены в результате сноса и выветривания:

Таким образом, высота будет определяться по формуле прямого определения угла наклона . Как видно, определение чревато большими ошибками. Пирамида Хефрена является исключением, потому что в верхней части до сих пор сохранились оригинальные замковые камни. Таким образом, угол может быть определен более точно, чем с другими пирамидами. Это объясняет хорошее согласие между различными авторами относительно угла наклона. ${\ displaystyle h}$${\ displaystyle \ beta}$${\ displaystyle \ beta}$

Это дает понять, что с настоящими пирамидами нельзя точно указать ни высоту до сантиметра, ни угол наклона до угловой секунды .

Связанные термины

Связанные геометрические формы - это усеченная пирамида ( пирамида, «срезанная» параллельно основанию) и двойная пирамида (многогранник, состоящий из двух зеркально-симметричных пирамид с одинаковым основанием).

Гипер пирамида является обобщением размеров. Пирамида, описанная в этой статье, представляет собой трехмерную гиперпирамиду. Двумерная гиперпирамида будет треугольником, четырехмерная - пентахороном . ${\ displaystyle n}$

Статья Пирамида (здание) посвящена пирамиде в архитектуре .

веб ссылки

• Эрик В. Вайсштейн : Пирамида . В: MathWorld (английский).