Мыльный пузырь

Мыльный пузырь представляет собой тонкую пленку из мыльной воды , что ловушки определенного количества воздуха или другого газа с образованием полой сферы , которая часто радужным и мерцающим. Мыльная пленка является плоской или изогнутой тонкой пленки, а мембрана из мыльной воды, например , зажимают в неподвижном кольце. Мыльная пена состоит из нескольких мыльных пузырей. Мыльные пузыри можно создавать сознательно, например, вдуванием воздуха в мыльную кожу, натянутую на кольцо.

Свежеприготовленные мыльные пузыри демонстрируют упругие колебания тела, иногда выделяют капли воды под действием силы тяжести, переносятся или переносятся воздушными потоками, все больше сохнут (если окружающий воздух не насыщен водой), со временем они становятся более чувствительными к стрессу от дуновение воздуха или даже контакт с (сухой) поверхностью другого тела. Мыльные пузыри часто лопаются через короткое время, иногда самопроизвольно.

Сохранение мыльных пузырей в воздухе в течение длительного времени, получение особых фигур или размеров - это предмет художественного ремесла. Мыльные пузыри являются объектами исследования физики, химии и геометрии и служат наглядной моделью для минимальных поверхностей .

Мыльные пузыри можно легко выдувать вручную, но также и с помощью машины. Они используются как сценический эффект и детская игра, но также и для взрослых как увлекательное и приятное времяпрепровождение или как физически интересное явление.

Из-за этой небольшой быстротечности «мыльный пузырь» стал метафорой чего-то привлекательного, но, тем не менее, бессмысленного и бессмысленного. Это отражено, например, во фразе «Мечта лопнула, как мыльный пузырь» или в синониме « экономика мыльного пузыря » для экономики пузыря .

В искусстве , по крайней мере с эпохи барокко, мыльный пузырь постоянно использовался иконографически как символ ваниты и отражает как красоту, так и непостоянство человеческой жизни.

Мыльные пузыри физически решают сложные пространственные задачи математики , поскольку в состоянии равновесия они образуют наименьшую поверхность между точками и краями.

строительство

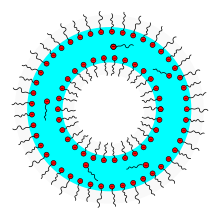
Мыльные пузыри состоят из тонкой ( диполярной ) пленки воды, на которой молекулы мыла прикрепляются внутри и снаружи с полярной гидрофильной карбоксилатной группой, обращенной к воде, и неполярным гидрофобным алкильным радикалом, обращенным от воды .

Структура похожа на структуру биомембран , но с мыльными пузырями вода находится внутри мембраны, а не за ее пределами.

быстротечность

Мыльный пузырь образуется при смешивании тонкой пленки воды с молекулами мыла. При надувании создается сферическая форма. В результате гравитационного стекания ( дренажа ) жидкости, находящейся между поверхностями мыльной пленки, мыльный пузырь в своей верхней части все больше истончается. Вы можете наблюдать это, когда натягиваете мыльную пленку на отверстие чашки, а затем держите ее вертикально. Кроме того, в процессе протечки молекулы ПАВ, стабилизирующие мыльную пленку , накапливаются в нижней части мыльного пузыря, так что его верхняя часть дополнительно дестабилизируется из-за относительного отсутствия молекул ПАВ, адсорбированных на поверхности. Фактически, большинство мыльных пузырей лопаются в верхней части. Испарению можно препятствовать, «заблокировав» мыльный пузырь или пленку мыла в каменной кувшине . Это значительно продлевает жизнь мочевого пузыря.

Можно наблюдать толщину слоя мыльного пузыря: если поверхность отражается красочными интерференционными цветами , толщина слоя сопоставима с длиной волны света. По мере уменьшения толщины слоя мыльная корка сначала будет бесцветной, а в конце темной.

В невесомости мыльные пузыри живут около одной минуты, в два раза дольше, чем на Земле. Стенка мочевого пузыря толще и ровнее и выдерживает укол иглой.

Физические основы

Поверхностное натяжение

Образование мыльных пузырей возможно, потому что поверхность жидкости - в данном случае воды - имеет поверхностное натяжение, которое приводит к упругому поведению поверхности. Часто считается, что мыло необходимо для увеличения поверхностного натяжения воды. Однако все обстоит наоборот: поверхностное натяжение мыльной воды составляет лишь около трети поверхностного натяжения воды. Создание мыльных пузырей из чистой воды настолько сложно, потому что поверхностное натяжение слишком велико, и пузырь мгновенно лопается. Кроме того, мыло замедляет испарение, благодаря чему пузырьки остаются дольше. Давление газа в мыльном пузыре выше, чем давление снаружи, см. Уравнение Юнга-Лапласа .

Сферическая форма

Поверхностное натяжение также является причиной сферической формы мыльных пузырей. Минимизируя площадь поверхности, он заставляет пузырек принимать эту форму, поскольку из всех возможных форм для данного объема сфера имеет наименьшую площадь поверхности. Без внешних сил (особенно силы тяжести в сочетании с трением воздуха ) все пузырьки имели бы идеальную сферическую форму. Мыльные пузыри из-за своего небольшого веса в реальности очень близки к этому идеалу.

Несколько связанных мыльных пузырей

Когда встречаются два мыльных пузыря, действуют те же принципы, и пузыри принимают форму с наименьшей площадью поверхности. Их общая стенка выпирает в больший пузырь, так как меньший мыльный пузырь имеет более высокое внутреннее давление. Если оба мыльных пузыря одинакового размера, выпуклости не будет и перегородка будет плоской.

Правила Плато гласят, что когда несколько мыльных пузырей собираются вместе, все углы одинаковы. В пенопласте с множеством пузырьков три поверхности всегда встречаются под углом 120 °. Поверхность здесь тоже минимальна. Такое же поверхностное натяжение создает равновесие сил . Четыре ребра встречаются под углом примерно 109 ° 28 '16 дюймов в узле , также известном как вершина . Эти правила были установлены в девятнадцатом веке на основе экспериментальных исследований бельгийского физика Жозефа Плато .

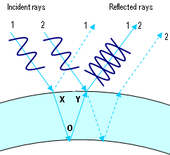
Отражение и вмешательство

В мерцающие цвета создаются помехи световых волн на тонкой коже мыло. Помехи приводят к удалению части цветового спектра в пределах определенного угла обзора . Остальная часть воспринимается в цвете, так как только полный цветовой спектр дает белый свет.

Поскольку стенка мыльного пузыря имеет определенную толщину, падающий свет отражается дважды - по одному с каждой стороны стены (см. Справа). Немного разные длины пути двух световых лучей (и специальные эффекты на внешней стене, см. Ниже) приводят к разнице в пути между ними. Если разность хода составляет ровно половину длины волны, впадины волн одного луча совпадают с гребнями волн другого (см. Второй рисунок). Итого результат нулевой, т.е. удаляется соответствующий цвет. Это называется деструктивной интерференцией, в отличие от конструктивной интерференции, при которой два луча накладываются друг на друга из-за разницы в пути (третье изображение).

Фактический цвет мыльного пузыря (т.е.длина волны погашенного света или длина разности хода) зависит от толщины мыльной пленки и угла освещения поверхности. Зависимость от толщины слоя можно наблюдать, когда мыльный пузырь истончается за счет испарения. По мере уменьшения толщины стираются другие цвета. В конечном счете, если толщина стены меньше половины наименьшей длины волны видимого света, никакие видимые световые волны не компенсируют друг друга, и дополнительные цвета больше не могут наблюдаться. В этом состоянии стенка мыльного пузыря тоньше двух десятитысячных миллиметра. При еще меньшей толщине слоя можно наблюдать темные пятна из-за других эффектов (см. Ниже) - они, вероятно, лопнут в следующий момент.

Предпосылка для интерференционных явлений - когерентность цугов волн - выполняется из-за толщины слоя. В дополнение к разной геометрической длине пути, еще один эффект также влияет на разницу в пути:

Волна, отраженная непосредственно на границе раздела воздух-мыльная кожа (точка X на втором рисунке), испытывает скачок фазы вокруг или в то время как фаза прошедшей волны остается неизменной даже после отражения на границе раздела мыльная кожа-воздух (точка O на диаграмму). Здесь нет скачка фазы. Вся разница в пути складывается из разной длины пути и скачка фазы при отражении на внешней границе раздела. ${\ displaystyle \ pi}$${\ displaystyle {\ tfrac {\ lambda} {2}}}$

Это также объясняет потемнение пузыря в момент непосредственно перед разрывом, когда толщина мыльной корки уменьшилась до очень небольшого значения: это связано с тем, что прошедшая волна, которая раньше проходила через мыло более длинным путем кожа, теперь практически никто не проходит большее расстояние, чем прямая отраженная волна, и поэтому не меняет своей фазы относительно этого. Однако отраженная волна испытала упомянутый выше скачок фазы, который приводит к деструктивной интерференции (подавлению) всех волн.

Если бы мыльный пузырь везде имел одинаковую толщину стенок, разница в траектории определялась бы только углом освещения, и он отображал бы равномерный цветовой градиент. Однако, поскольку пленка жидкости в мыльном пузыре, который движется через воздушный поток, закручивается за счет трения воздуха, толщина стенки неоднородна. При благоприятных условиях эти завихрения можно увидеть невооруженным глазом. Однако, если мыльный пузырь плавает относительно спокойно, происходит только несколько турбулентностей: вы можете наблюдать отдельные, относительно ровные цветные полосы. В основном существующие колебания толщины из-за силы тяжести относительно однородны и в принципе не нарушают однородный цветовой градиент.

Эти цвета легче увидеть на плоской мыльной пленке. Такая плоская пленка может, например, Б. формироваться в прямоугольной или круглой оправе из тонких полимерных волокон или тонкой проволоки. Оптимальные условия для видимости интерференционных цветов - непрямое освещение (например, лист белой бумаги, освещенный галогенной лампой) с углом падения 45 градусов и наблюдение в отражении под углом отражения 45 градусов. Фон за мыльной пленкой должен быть темным.

По краям пленка образует мениск с рамкой или резервуаром для жидкости в нижней части пленки. В последнем случае сочетание гравитации и капиллярной силы является движущей силой, которая вызывает неоднородную толщину пленки.

Турбулентность и эстетические движущиеся узоры в области мениска и на краях с рамкой вызваны гидродинамической нестабильностью, в которой, скорее всего, важную роль играет эффект Марангони .

Замороженные мыльные пузыри

Мембрана мыльного пузыря может замерзать при низких температурах, не разрываясь. Это происходит с вылетающими мыльными пузырями при температуре ниже −10 ° C на открытом воздухе или с прилипшими мыльными пузырями в морозильной камере. Они стабильны до 10 минут. Иногда замороженные мыльные пузыри могут выжить при приземлении на твердые и холодные поверхности.

Замораживание мыльного пузыря, лежащего на снегу, обычно происходит из-за роста кристаллов, похожих на оперение, из соседнего снега, который действует как микроб, и может длиться около 2 секунд.

использовать

Показывает

Шоу мыльных пузырей сочетают в себе развлечение и артистичность. Это требует высокого уровня мастерства, а также идеальных решений для мыльных пузырей.

Примеры распространенных выступлений:

• огромные мыльные пузыри, которые часто содержат предметы или людей,
• Обработка мыльных пузырей голыми руками,
• угловатые мыльные пузыри в форме кубов , тетраэдров и т. д.,
• Соединяйте несколько пузырей с более сложными конструкциями или скульптурами.
• Визуально привлекательные эффекты, например, пузыри, наполненные дымом, или использование лазерного света ,
• с пузырьками, наполненными гелием, которые всплывают вверх,
• Связь мыльных пузырей и огня.

Мыльные пузыри в математике

Мыльная пленка образует естественную минимальную поверхность . Математические исследования были сосредоточены на минимальных областях с 19 века. Существенный вклад в это внесли эксперименты бельгийского физика Жозефа Плато (см. Задачу Плато ).

Пример: Герман Амандус Шварц еще в 1884 году доказал, что сферический мыльный пузырь имеет наименьшую возможную площадь поверхности определенного объема воздуха. Однако только в последние несколько десятилетий подходящий язык для таких задач был найден с помощью геометрической теории измерения . В 2000 году вслед за Майклом Хатчингсом , Фрэнком Морганом , Мануэлем Риторе и Антонио Росом удалось доказать, что два связанных пузырька (так называемый двойной пузырь ), охватывающие два объема воздуха разного размера с наименьшей возможной площадью поверхности (также теорема о двойном пузыре ; английская теорема о двойном пузыре) ).

Мыльные пузыри в архитектуре

Долгое время мыльные пузыри были единственным средством надежного определения оптимального уклона нетривиальных кровельных конструкций на основе вантовых систем и несущих арок. Для этого конструкция была сделана в виде каркаса из проволоки и затем погружена в мыльную воду. Осторожное выдергивание привело к кривым, которые можно было считать экспериментально найденным оптимумом формы. Результат был зафиксирован фотографией и другими методами и перенесен на соответствующие строительные чертежи. Соответствующая статика для данной формы затем может быть определена другими методами. Одним из примеров этой методологии является олимпийский объект в Мюнхене .

Мыльные пузыри игрушки

Одно из самых ранних художественных изображений мыльных пузырей в виде детских игрушек можно найти в картине Питера Брейгеля « Детские игры» 1560 года, в которой говорится, что мыльные пузыри использовались детьми для развлечения не менее 500 лет. Массовое производство мыла началось в 19 веке, когда производитель мыла Pears использовал для маркетинга, в частности, картину Джона Эверетта Милле « Мыльные пузыри» («Bubbles»), на которой его внуки играют с мыльными пузырями.

В 1948 году химик Рольф Хайн разработал новую формулу моющего средства, которое, однако, имело недостаток - слишком сильное пенообразование. Он разлил жидкое мыло в бутылки, добавил кольцо для надувания из тонкой пружинной проволоки с ручкой, согнутой в кольцо, и продал продукт специально как детскую игрушку под торговой маркой Pustefix . С тех пор для производства мыльных пузырей в основном использовались комбинации пластиковых трубок, наполненных щелочью, и колец для пустышки.

литература

• CV Boys : Мыльные пузыри. Их цвета и силы, которые их формируют . Dover Publications, Нью-Йорк 1990, ISBN 0-486-20542-8
• Ханнелоре Диттмар-Ильген: Почему лопаются мыльные пузыри? Физика для любознательных . Hirzel-Verlag, Штутгарт 2003, ISBN 3-7776-1149-2
• Сириэль Изенберг: Наука о мыльных пленках и мыльных пузырях . Tieto Books, Clevedon North Somerset 1978, ISBN 0-905028-02-3
• J. Vogel: Gerthsen Physik . Учебник Springer. Springer Verlag, Гейдельберг
• CV Мальчики: Мыльные пузыри и силы, которые их формируют , природа и знания, Том W 13, Деш, Мюнхен 1961

веб ссылки

• Эксперименты
• Доказательство теоремы о двойном пузыре
• История мыловарения

Индивидуальные доказательства

1. ↑ science.ORF.at/AFP: Мыльные пузыри дольше живут в космосе. В: science.ORF.at. 9 июля 2014, доступ к 9 июля 2014 . 
2. ↑ Сэм Уотонс: Исследователи проверяют теорию пузырей в условиях невесомости, Интернет на сайте timesnews.net
3. ↑ Эшли Леонард: Как сделать пузырь, который не лопнет ehow.com, без даты, по состоянию на 24 января 2017 г.
4. ↑ Замораживающие мыльные пузыри, сфотографированные на снегу ... pilleus pulcher, google +, 23 января 2017 г., по состоянию на 25 января 2017 г. - Серия изображений.
5. ↑ Майкл Хатчингс; Фрэнк Морган; Мануэль Риторе; Антонио Рос: Доказательство гипотезы о двойном пузыре . В: Announc. Амер. Math. Soc. , 2000, 6 с. 45-49, pdf .
6. ↑ Ансгар Мёнтер: Тот, у кого мыльный пузырь. В: nw.de . 17 августа 2011 г., по состоянию на 11 декабря 2020 г.
7. ↑ История Pustefix. В: pustefix.de. Проверено 6 июня 2019 года . 

	Эта статья доступна в виде аудиофайла:
	Сохранить | Информация  | 11:39 мин (3,1 МБ) текст разговорной версии (27 сентября 2004 г.)
	Больше информации в устной Википедии.