Куб (геометрия)

куб
Тип боковых поверхностей	Квадраты
Количество лиц	6-е
Количество углов	8-е
Количество ребер	12-е
Значок Schläfli	{4.3}
двойной к	октаэдр
Сеть тела
Количество разных сетей	11
Количество граней в углу	3
Количество углов поверхности	4-й
Кубики в формате STL

Куб (немецкого бросок , потому что он брошен в кости игры, также регулярный шестигранник [ hɛksaeːdər ], от греческого. Hexáedron , шестигранника «или куб , из древнегреческого κύβος kybos или лат. Cubus , куб») является одним из пять Платоновых тел , точнее трехмерный многогранник ( многогранник ) с

• 6 одинаковых квадратов в качестве боковых граней
• 12 ребер одинаковой длины и
• 8 углов , в каждом из которых сходятся по три боковые поверхности.

Куб - это особый трехмерный параллелепипед , особый, а именно равносторонний кубоид и особая прямая квадратная призма . Размеры куба уже определены путем указания значения, длины ребра, диагонали поверхности, пространственной диагонали, площади поверхности или объема .

симметрия

Куб в проекции шкафа (диметрия)
с примерами осей вращения и зеркальных плоскостей (красная и зеленая)${\ displaystyle C_ {2}, C_ {4}, C_ {3}}$

Из-за своей высокой симметрии - все углы , ребра и стороны похожи друг на друга - куб является правильным многогранником . Он имеет

• 3 оси вращения четвертого порядка (через центры двух противоположных поверхностей ),${\ displaystyle C_ {4}}$
• 4 тройные оси вращения (через два диагонально противоположных угла),${\ displaystyle C_ {3}}$
• 6 осей двойного вращения (через центры двух диагонально противоположных граней),${\ displaystyle C_ {2}}$
• 9 зеркальных уровней (6 уровней через четыре угла каждый (например, зеленый), 3 уровня через четыре центра краев каждый (например, красный)),
• 14 поворотов (6 на 90 ° с плоскостями через четыре краевых центра каждое и 8 на 60 ° с плоскостями через шесть краевых центров каждое)

и является

• точка симметрично к центру М.

Для четырехугольной оси вращения есть 3 операции симметрии ( поворот на 90 °, 180 ° и 270 °), для трехкратной оси вращения соответственно 2 операции симметрии. Всего в группе симметрии куба 48 элементов. Они называется в Шенфлисе нотации , как в Hermann / Mauguin в нотации , как и в целом, но несколько неточным, так как октаэдрические группы или куб группы. ${\ displaystyle O_ {h}}$${\ Displaystyle 4 / м \ {\ бар {3}} \ 2 / м}$

Отношения с другими многогранниками

Куб с двойным октаэдром. В центрах квадратов являются углами октаэдра.

Куб - это многогранник, двойственный октаэдру, и наоборот. Кроме того, угловые точки куба описывают два точечно-симметричных правильных тетраэдра , которые вместе образуют звездный тетраэдр как дополнительный правильный многогранник .

С помощью куба и октаэдра можно построить множество тел , которые также имеют группу куба в качестве группы симметрии . Так вы, например, получите

• усеченный шестигранник или усеченный куб с 6 восьмиугольника и 8 треугольников
• кубооктаэдр с 6 квадратов и 8 треугольников, т.е. 14 сторон, и 12 углов
• усеченный октаэдр или усеченного октаэдра с 6 квадратов и 8 шестиугольников

как пересечение куба с октаэдром (см. архимедовы тела ) и

• ромбического додекаэдра с 6 + 8 = 14 углов и 12 пастилок как сторон

как выпуклая оболочка объединения куба с октаэдром.

Куб является составной частью регулярной мозаики куба .

Формулы

Размеры куба с длиной ребра а
объем	${\ Displaystyle \, V = а ^ {3}}$	без зарегистрированных углов
Внешняя поверхность	${\ Displaystyle A_ {M} = 4 \ cdot a ^ {2}}$
Площадь поверхности	${\ displaystyle A_ {O} = 6 \ cdot a ^ {2}}$
Умкугельрадиус	${\ displaystyle r_ {u} = {\ frac {a} {2}} \ cdot {\ sqrt {3}} \ приблизительно 0 {,} 866 \ cdot a}$
Радиус краевого шара	${\ displaystyle r_ {k} = {\ frac {a} {2}} \ cdot {\ sqrt {2}} \ приблизительно 0 {,} 707 \ cdot a}$
Inc радиус сферы	${\ displaystyle r_ {i} = {\ frac {a} {2}} = 0 {,} 5 \ cdot a}$
Диагональ комнаты	${\ displaystyle d_ {R} = 2 \ cdot r_ {u} = a \ cdot {\ sqrt {3}} \ приблизительно 1 {,} 732 \ cdot a}$
Диагональ поверхности	${\ displaystyle d_ {F} = 2 \ cdot r_ {k} = a \ cdot {\ sqrt {2}} \ приблизительно 1 {,} 414 \ cdot a}$
Отношение объема  к сферическому объему	${\ displaystyle {\ frac {V} {V_ {UK}}} = {\ frac {2 \ cdot {\ sqrt {3}}} {3 \ cdot \ pi}} \ приблизительно 0 {,} 368}$
Угол между смежными гранями / кромками	${\ Displaystyle \ альфа, \ бета = 90 ^ {\ circ}}$
Сплошные углы в углах	${\ displaystyle \ Omega = {\ frac {\ pi} {2}} \; \ mathrm {sr} \; \ приблизительно 1 {,} 5708 \; sr}$
Сферичность	${\ displaystyle \ Psi = {\ sqrt [{3}] {\ frac {\ pi} {6}}} \ приблизительно 0 {,} 806}$

Сплошные углы в углах

Телесный угол в центре  (точка = 0) единичной сферы ( )${\ displaystyle \ Omega}$${\ Displaystyle \ mathrm {M}}$${\ displaystyle r = 1}$

Этот телесный угол очень легко получается из рассмотрения следующей ситуации. ${\ displaystyle \ Omega}$

Для трехмерного пространства используется декартова система координат , пространство в 8 октантах делится. Точка 0 трех координатных плоскостей (x, y, z) - это точка встречи 8 виртуальных кубов. С точкой 0 в качестве центра единичной сферы , телесный угол (полный угол) имеет значение Принимая во внимание, его телесный угол, таким образом, отсчитывается от точки 0, начиная только с 1 кубика, и применяется указанная единица измерения.${\ displaystyle 4 \ pi.}$${\ displaystyle {\ frac {4 \ pi} {8}}.}$

${\ displaystyle \ Omega = {\ frac {\ pi} {2}} \; \ mathrm {sr} \; \ приблизительно 1 {,} 570796327 \; \ mathrm {sr}}$

Определение как набор точек

Куб может быть определена как набор из точек в трехмерном евклидовом пространстве , где абсолютные значения 3 координат в системе декартовых координат являются не более , как большой , как радиус сферы вкл . Формально эту сумму можно записать как ${\ displaystyle r_ {i} = {\ tfrac {a} {2}}}$

${\ displaystyle \ left \ {x \ in \ mathbb {R} ^ {3} \ mid \ left \ | x \ right \ | _ {\ infty} \ leq r_ {i} \ right \} = \ left \ { (x_ {1}, x_ {2}, x_ {3}) \ mid \ max _ {i = 1,2,3} | x_ {i} | \ leq r_ {i} \ right \}}$

Вот максимальная норма или бесконечная норма вектора . Применяется для внутренней части куба и для поверхности . Согласно этому определению, центр куба является началом координат, а его ребра и грани проходят параллельно 3 осям декартовой системы координат . ${\ Displaystyle \ влево \ | х \ вправо \ | _ {\ infty}}$ ${\ displaystyle x}$${\ Displaystyle \ влево \ | х \ вправо \ | _ {\ infty} <r_ {я}}$${\ Displaystyle \ влево \ | х \ вправо \ | _ {\ infty} = r_ {я}}$

В более общем смысле куб, который занимает любую позицию в трехмерном евклидовом пространстве, может быть определен с помощью векторов . Является ли вектор положения в центре и , , ортогональные векторы направления , соединяющий центр куба с центрами 3 боковых поверхностей соединить, поэтому нормальные векторами являются 3 боковыми поверхностями и ортогональная система из трехмерной векторного пространства формы, то листы количество из точек кубы определяется как множество векторов${\ displaystyle {\ vec {m}}}$${\ displaystyle {\ vec {u}}}$${\ displaystyle {\ vec {v}}}$${\ displaystyle {\ vec {w}}}$ ${\ Displaystyle \ mathbb {R} ^ {3}}$

${\ displaystyle \ left \ {{\ vec {m}} + t_ {1} \ cdot {\ vec {u}} + t_ {2} \ cdot {\ vec {v}} + t_ {3} \ cdot { \ vec {w}} \ in \ mathbb {R} ^ {3} \ mid \ left \ | t \ right \ | _ {\ infty} \ leq r_ {i} \ right \} = \ left \ {{\ vec {m}} + t_ {1} \ cdot {\ vec {u}} + t_ {2} \ cdot {\ vec {v}} + t_ {3} \ cdot {\ vec {w}} \ in \ mathbb {R} ^ {3} \ mid \ max _ {i = 1,2,3} | x_ {i} | \ leq r_ {i} \ right \}}$

обобщение

Обобщения куба в любом измерении также называются -мерными кубами или гиперкубами и также являются правильными многогранниками . - Мерный куб имеет ограничение стороны размерности к. Особые случаи: ${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle 2 ^ {nk} \ cdot {\ tbinom {n} {k}}}$

• Нульмерный куб ( точка ) имеет 1 угол .
• Одномерный куб ( отрезок ) имеет 2 угла.
• Двумерный куб ( квадрат ) имеет 4 угла и 4 ребра.
• Четырехмерный гиперкуб ( тессеракт ) имеет 16 углов, 32 ребер, 24 боковых квадраты и 8 боковых кубики.
• -Мерном гиперкуб имеет ${\ displaystyle n}$
  • ${\ Displaystyle 2 ^ {п}}$Углы ( )${\ displaystyle k = 0}$
  • ${\ Displaystyle п \ cdot 2 ^ {п-1}}$Края ( )${\ displaystyle k = 1}$
  • ${\ Displaystyle п \ cdot (п-1) \ cdot 2 ^ {п-3}}$ Квадраты как площади ( )${\ displaystyle k = 2}$
  • ${\ Displaystyle {\ tfrac {1} {3}} \ cdot n \ cdot (n-1) \ cdot (n-2) \ cdot 2 ^ {n-4}}$Куб как объем ( )${\ displaystyle k = 3}$
  • ${\ displaystyle 2 \ cdot n}$ Гиперкубы измерения как
  фасеты ( ).${\ displaystyle n-1}$${\ Displaystyle к = п-1}$

Модель -мерного куба - это единичный куб в векторном пространстве . И это готовый единичный куб. ${\ displaystyle n}$ ${\ displaystyle I ^ {n}}$ ${\ Displaystyle \ mathbb {R} ^ {п}}$

• ${\ displaystyle I ^ {n} = \ left \ {(x_ {1}, \ dots, x_ {n}) \ mid 0 \ leq x_ {i} \ leq 1 \ right \}}$
• ${\ Displaystyle I ^ {п} = [0,1] \ раз \ cdots \ раз [0,1]}$, То -кратно декартово произведение на единичный интервал${\ displaystyle n}$
• выпуклая оболочка в угловых точках с координатами и${\ Displaystyle 2 ^ {п}}$ ${\ displaystyle 0}$${\ displaystyle 1}$
• пересечение с полупространствами и${\ displaystyle 2n}$ ${\ displaystyle x_ {i} \ geq 0}$${\ Displaystyle х_ {я} \ leq 1}$

Единичный куб - это параллельный оси куб с длиной ребра и углом в начале координат . Обобщением этой концепции являются кубоиды im , которые играют роль в многомерном анализе .${\ displaystyle 1}$${\ Displaystyle \ mathbb {R} ^ {п}}$

Сети куба

В кубе одиннадцать сеток (см. Иллюстрацию). Это некие гексомино . Это означает, что есть одиннадцать способов развернуть полый куб, разрезав 7 граней и разложив его на плоскости . Остальные 5 ребер соединяют 6 квадратов сети. Для того, чтобы раскрасить куб так, чтобы все соседние грани не были одного цвета, вам понадобится как минимум 3 цвета.

Анимация кубической сети

Различные сети куба

Графики, двойственные графики, циклы, цвета

Куб имеет неориентированный плоский граф с 8 узлами , 12 ребрами и 6 областями, назначенными ему, который является 3- регулярным , то есть 3 ребра начинаются от каждого узла, так что степень равна 3 для всех узлов. В случае плоских графов точное геометрическое расположение узлов не имеет значения. Однако важно, чтобы края не пересекались. Узлы этого кубического графа соответствуют углам куба.

Раскраска изображает
куб, описывающий двойной октаэдр.

В узлах куба графа могут быть окрашены с 2 -х цветов , так что соседние узлы всегда окрашены по- разному. С помощью этого переменного узла цвета, цвет меняется назад и вперед , когда вы переходите от одного узла к примыкающим один . Это означает, что хроматическое число этого графа равно 2. Кроме того, края можно раскрасить в 3 цвета, чтобы смежные края всегда были окрашены по-разному (см. Иллюстрацию). Это невозможно с 2 цветами, поэтому хроматический индекс для окраски краев равен 3 (рисунок справа иллюстрирует эту окраску).

Чтобы определить необходимое количество цветов для областей или областей, полезен двойной граф (восьмеричный граф ) с 6 узлами , 12 ребрами и 8 областями. Узлы этого графа назначаются взаимно однозначно (биективно) областям кубического графа и наоборот (см. Биективную функцию и рисунок выше). Узлы графа октадера могут быть окрашены в 3 цвета, так что соседние узлы всегда окрашиваются по-разному, но не 2 цветами, так что хроматическое число графа октад составляет 3. Из этого можно сделать косвенный вывод: поскольку хроматическое число равно 3, для такой раскраски поверхности куба или раскраски областей графа куба необходимо 3 цвета.

Узловая раскраска кубического графа

Раскраска ребер кубического графа

Раскраска площадей кубического графа с двойной раскраской узлов графа октаэдра

7 обрезанных ребер каждой сети (см. Выше) вместе с углами ( узлами ) образуют остовное дерево кубического графа . Каждая сеть точно соответствует покрывающему дереву и наоборот, так что между сетями и покрывающими деревьями существует взаимно однозначное ( биективное ) присвоение. Если вы рассматриваете сеть кубов без внешней области как граф, вы получаете двойной граф с деревом с 6 узлами и 5 ребрами и максимальной степенью узлов 4. Каждая область куба назначается узлу дерева. . Каждое теоретико-графовое созвездие (см. Изоморфизм графов ) таких деревьев встречается, некоторые также несколько раз.

В графе куба 12 кругов Гамильтона , но нет кругов Эйлера .

Куб граф Гамильтон цикл

Срезанные поверхности куба

Если куб вырезан из плоскости, поверхность разреза может быть треугольником , квадратом , (неправильным) пятиугольником или шестиугольником . В качестве поверхности среза также возможны равносторонний треугольник , квадрат или правильный шестиугольник.

Срезать поверхность в форме правильного пятиугольника - без параллельных сторон - невозможно, так как две поверхности в кубе параллельны друг другу.

• 

  Равносторонний треугольник как поверхность среза

• 

  Квадрат как поверхность среза

• 

  Правильный шестиугольник как поверхность среза

• 

  Неправильный пятиугольник как поверхность среза

Кубическая сетка

Конечная часть кубической поверхностной решетки (кубическая решетка), имеющая форму кубоида . Эти самолеты работать параллельно друг с другом. На прямой линии пересечения этих плоскостей идут параллельно друг другу. В точках пересечения образуют кубическую решетку точки .

Кубическая сетка представляет собой расположение бесконечного числа точек в трехмерном евклидовом пространстве . Эти точки можно рассматривать как все точки в трехмерной декартовой системе координат , где все 3 координаты являются целыми числами . Этот набор точек можно формально назвать множеством

${\ displaystyle \ left \ {(x_ {1}, x_ {2}, x_ {3}) \ in \ mathbb {R} ^ {3} \ mid x_ {1} \ in \ mathbb {Z} \ \ land \ x_ {2} \ in \ mathbb {Z} \ \ land \ x_ {3} \ in \ mathbb {Z} \ right \}}$

быть написанным.

Эта кубическая решетка является аксиально симметричной , осесимметричной и точкой симметрии , так что она имеет все симметрии в группе октаэдра или куба группы. Кроме того, это трансляционной симметрии для всех векторов с целым длины , которые проходят параллельно 3 осям координат, то есть бесконечное число векторов , , , , где , , являются целыми числами и , , в 3 единичные векторы в трехмерном eudklidischen векторное пространство . ${\ displaystyle a_ {1} \ cdot {\ vec {e}} _ {1}}$${\ displaystyle a_ {2} \ cdot {\ vec {e}} _ {2}}$${\ displaystyle a_ {3} \ cdot {\ vec {e}} _ {3}}$${\ displaystyle a_ {1}}$${\ displaystyle a_ {2}}$${\ displaystyle a_ {3}}$ ${\ displaystyle e_ {1}}$${\ displaystyle e_ {2}}$${\ displaystyle e_ {3}}$

Такие соображения играют важную роль в кристаллографии . Кубическая решетка соответствует кубической кристаллической системе .

Если бесконечное количество параллельных плоскостей , каждая на расстоянии 1, размещается перпендикулярно трем координатным осям через эту кубическую сетку точек , то создается кубическая сетка поверхностей (см. Иллюстрацию). Эти уровни могут быть более формальными, чем установленные

${\ Displaystyle \ left \ {(x_ {1}, x_ {2}, x_ {3}) \ in \ mathbb {R} ^ {3} \ mid x_ {1} \ in \ mathbb {Z} \ \ lor \ x_ {2} \ in \ mathbb {Z} \ \ lor \ x_ {3} \ in \ mathbb {Z} \ right \}}$

быть написанным.

Если трехмерное пространство также полностью заполнено, трехмерная мозаика ( заполнение комнаты ) создается из конгруэнтных кубов с одинаковой длиной ребра (см. Заполнение комнаты кубами ).

Удвоение куба

Синий куб имеет в два раза объем зеленого куба.

Удвоение куба , также известный как проблема гастроном в описывает геометрическую задачу построения второго куба для данного куба , который имеет в два раза объем первого куба . Задача принадлежит к трем « классическим задачам античной математики » и возникла уже в V веке до нашей эры. Создан в Древней Греции .

Если вы попытаетесь работать над проблемой исключительно с помощью вспомогательных средств, которые Евклид использует в своих элементах , а именно с помощью циркуля и линейки без опознавательных знаков , решить ее не удастся. Французский математик Пьер Ванцель доказал это в 1837 году. Если это ограничение ослабить и допустить дополнительную помощь, такую ​​как соответствующая отметка на линейке или специальные кривые, можно построить куб с удвоенным объемом. Некоторое количество таких возможных решений было известно еще в древности.

Комната заполняется кубиками

Трехмерное евклидово пространство может быть полностью заполнено с многогранниками или в комбинации с архимедовыми твердых (и призмами ) одной и той же длиной кромки. Такое трехмерное плиточные это называется наполнение комнаты . Следующие заливки комнаты содержат кубики:

• 

  Наполнение комнаты кубиками

• 

  Заполнение помещения ромбическим кубооктаэдром , кубооктаэдром и кубом

• 

  Заполнение комнаты ромбическим кубооктаэдром, кубом и тетраэдром

• 

  Заполнение помещения усеченным шестигранником , ромбическим кубооктаэдром, восьмиугольной призмой и кубом

• 

  Заполнение помещения большим ромбическим кубооктаэдром , усеченным октаэдром и кубом

Связь с другими наполнителями комнаты

Куб или правильный шестигранник - единственное платоново твердое тело, которое можно использовать для заполнения пространства исключительно конгруэнтными многогранниками . В углах этих кубиков одинакового размера , то образуют куб сетку . Этот заряд камеры связан с двумя другими зарядами камеры, которые состоят только из конгруэнтных многогранников: пространство, заполненное усеченными октаэдрами (английский: bitruncated cubic honeycomb ), и пространство, заполняющее Rhombendodekaedern (английский: ромбические додекаэдрические соты ).

Если взять чередующееся заполнение половины комнаты кубиками длины ребра , т.е. каждый 2-й куб заполнения комнаты, и квадратную пирамиду с квадратом длины стороны и высоты наружу разместить на всех квадратных боковых поверхностях куба, то конгруэнтно ромбические додекаэдры созданы , которые формируют номера заливки в полностью. Двугранный угол на базу из квадратных пирамид это все приводит к краям 12 куба углу так . Таким образом, 24 равнобедренных треугольника, лежащих на краях куба, образуют 12 ромбов и образуется ромбический додекаэдр. Согласно теореме Пифагора , эти ромбические додекаэдры имеют длину ребра и, очевидно, объем . С помощью формулы для объема квадратной пирамиды это тоже получается (см. Анимацию).${\ displaystyle a}$${\ displaystyle a}$ ${\ Displaystyle {\ tfrac {а} {2}}}$ ${\ displaystyle \ arctan \ left ({\ frac {\ tfrac {a} {2}} {\ tfrac {a} {2}}} \ right) = \ arctan (1) = 45 ^ {\ circ}}$${\ displaystyle 90 ^ {\ circ} +2 \ cdot 45 ^ {\ circ} = 180 ^ {\ circ}}$${\ Displaystyle {\ tfrac {а} {2}} \ cdot {\ sqrt {3}}}$ ${\ displaystyle 2 \ cdot a ^ {3}}$${\ displaystyle a ^ {3} +6 \ cdot \ left ({\ tfrac {1} {3}} \ cdot a ^ {2} \ cdot {\ tfrac {a} {2}} \ right) = 2 \ cdot a ^ {3}}$

Если вместо этого, только кубики из чередующихся рядов будут взяты из чередующегося заполнения половины комнаты - независимо от того, какое из трех измерений - то есть каждый 4-й куб исходного заполнения комнаты, каждый квадрат под углом 45 ° с половиной площади в середина Помещается между двумя соседними кубами одного и того же слоя, и углы этих квадратов, которые находятся ближе всего друг к другу, соединяются ребрами, затем конгруэнтные усеченные октаэдры с 6 квадратами каждый и 8 правильных шестиугольников в качестве боковых поверхностей , полностью заполнить в пространстве . В центрах в результате правильных шестиугольников являются углами исходных кубов. Углы квадратных боковых поверхностей усеченных октаэдров являются боковыми центрами «невидимых» квадратов с длиной стороны . Таким образом, усеченные октаэдры имеют длину ребра и, очевидно, объем . С помощью формулы для объема квадратной пирамиды это тоже получается (см. Анимацию). ${\ displaystyle a}$${\ Displaystyle {\ tfrac {а} {2}} \ cdot {\ sqrt {2}}}$ ${\ displaystyle 4 \ cdot a ^ {3}}$${\ displaystyle 2 \ cdot \ left ({\ tfrac {1} {3}} \ cdot \ left (3 \ cdot {\ tfrac {a} {2}} \ cdot {\ sqrt {2}} \ right) ^ {2} \ cdot \ left (3 \ cdot {\ tfrac {a} {2}} \ right) \ right) -6 \ cdot \ left ({\ tfrac {1} {3}} \ cdot \ left ({ \ tfrac {a} {2}} \ cdot {\ sqrt {2}} \ right) ^ {2} \ cdot {\ tfrac {a} {2}} \ right) = 2 \ cdot \ left ({\ tfrac {9} {4}} \ cdot a ^ {3} \ right) -6 \ cdot \ left ({\ tfrac {1} {12}} \ cdot a ^ {3} \ right) = 4 \ cdot a ^ {3}}$

• 

  Наполнение комнаты кубиками

• 

  Переменный половина наполнения комнаты с кубиками создает начинку комнаты , изготовленную из конгруэнтных ромбических додекаэдров

• 

  Переменная четвертовали наполнение комнаты с кубиками создает начинку номера , выполненную из конгруэнтен усеченного октаэдра

Мастерство

Вставленный куб

Из более сотни спичек можно сделать кубики, которые держатся вместе простым зажимом и трением.

• 

  Игральные кости спички

• 

  Кубики оригами

оригами

С помощью техники оригами кубик можно сделать из отдельных листов бумаги без использования клея.

Токарный станок

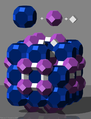
На токарном станке для металлорежущей обработки куб можно также изготавливать в трехкулачковом патроне с использованием четырехкулачкового патрона или мягкого трубчатого держателя. Превратить комбинацию из четырех незакрепленных, но невнятных кубиков, один внутри другого, - задача мастерства . Эта заготовка по-английски называется кубиком токаря . У трех внешних кубов есть большие отверстия с каждой стороны, которые, как окно, позволяют видеть следующий или следующий внутри. Размеры трех внутренних кубов рассчитаны таким образом, чтобы даже диагональная поверхность не проходила через это отверстие в следующем, более крупном кубе. Необходимо подрезать каждую сторону внутренних кубиков и временно закрепить их клеем или воском, если шестая сторона будет обрабатываться в последнюю очередь.

Смотри тоже

• Сеть кубов
• Удвоение куба
• Числа куба
• Дидервинкель
• многогранник
• Платоново твердое тело

веб ссылки

• Евклид: Stoicheia. Книга XIII.15. Куб сферы
• Представление косых изображений, центральных проекций, сетей и сечений кубов
• Пазл для пространственной концепции кубиков
• интерактивное отображение многомерных кубов

Индивидуальные доказательства

1. ↑ Сусуму Онака, Департамент материаловедения и инженерии, Токийский технологический институт: простые уравнения, определяющие формы различных выпуклых многогранников: правильных многогранников и многогранников, составленных из кристаллографически малоиндексной плоскости
2. ^ Мартин Хенк, Юрген Рихтер-Геберт, Гюнтер М. Циглер, Технический университет Берлина: Основные свойства выпуклых многогранников
3. ↑ Wolfram Demonstrations Project: Все 11 складных сетей куба
4. ↑ C.Dalfó, MA Fiol: Графики, друзья и знакомые. (PDF) 2. Рукопожатие: раскраски и булева алгебра. Universitat Политекника Каталунья, Departament де Matematica Aplicada IV, 2010, стр. 5 , доступ к 31 мая 2020 года . 
5. ↑ Ричард Голдстоун, Роберт Суззи Валли: Развертывание куба . В: Журнал математики колледжа . Лента 50 , нет. 3 , 28 мая 2019 г., ISSN  0746-8342 , стр. 173-184 , DOI : 10,1080 / 07468342.2019.1580108 ( researchgate.net [PDF]). 
6. ^ Wolfram Math World: кубический график
7. ^ Wolfram MathWorld: Кубическая решетка
8. ↑ Проф. Хольгер Кольманн, Лейпцигский университет: Теория групп 2 и 3 - Теория групп в кристаллографии
9. ↑ Ханс Смессерт, logicgeometry.org: Логическая геометрия ромбического додекаэдра оппозиций
10. ↑ themetalcutter: Куб в кубе / Turners cube youtube.com, видео (43:07) от 19 августа 2015 г., доступ 17 марта 2017 г.