Одноэтапный процесс

Одношаговые методы аппроксимируют решение (синий цвет) задачи с начальным значением, определяя точки и т. Д., Одну за другой от заданной начальной точки.${\ displaystyle A_ {0}}$${\ displaystyle A_ {1}}$${\ displaystyle A_ {2}}$

В вычислительной математике одношаговые методы , помимо многошаговых, представляют собой большую группу вычислительных методов для решения задач с начальным значением . Эта задача, в которой общее дифференциальное уравнение задается вместе с исходным условием, играет центральную роль во всех естественных и технических науках и становится все более важной, например, в экономике и социальных науках. Задачи начального значения используются для анализа, моделирования или прогнозирования динамических процессов.

Именная основная идея одношагового метода состоит в том, что, начиная с заданной начальной точки, шаг за шагом вычисляют точки аппроксимации по искомому решению. При этом они используют только последнее определенное приближение для следующего шага, в отличие от многоступенчатого метода, который также включает точки, которые находились дальше назад в вычислении. Одношаговые методы можно условно разделить на две группы: явные методы, которые вычисляют новое приближение непосредственно из старого, и неявные методы, в которых необходимо решить уравнение. Последние также подходят для так называемых жестких задач с начальным значением.

Самый простой и старый одношаговый метод, явный метод Эйлера , был опубликован в 1768 году Леонардом Эйлером . После того, как в 1883 году была представлена ​​группа многоступенчатых процессов, примерно в 1900 году Карл Рунге , Карл Хойн и Вильгельм Кутта разработали значительные усовершенствования процесса Эйлера. Из них возникла большая группа процессов Рунге-Кутта , которые составляют наиболее важный класс одношаговых процессов. Дальнейшие разработки 20-го века - это, например, идея экстраполяции , но прежде всего соображения для управления размером шага, то есть для выбора подходящей длины для отдельных шагов метода. Эти концепции составляют основу для решения сложных задач начального значения, которые возникают в современных приложениях, эффективно и с необходимой точностью с использованием компьютерных программ.

вступление

Обыкновенные дифференциальные уравнения

Развитие дифференциального и интегрального исчисления английским физиком и математиком Исааком Ньютоном и независимо от него немецким эрудитом Готфридом Вильгельмом Лейбницем в последней трети 17 века послужило важным импульсом для математизации науки в период раннего Нового времени . Эти методы стали отправной точкой математической отрасли анализа и имеют центральное значение во всех естественных и технических науках. В то время как Лейбниц руководствовался геометрической проблемой определения касательных к заданным кривым в дифференциальном исчислении, Ньютон исходил из вопроса о том, как можно определить изменения физической величины в определенный момент времени.

Например, когда тело движется, его средняя скорость - это просто пройденное расстояние, разделенное на время, которое оно потребовало. Однако для того, чтобы математически сформулировать текущую скорость тела в определенный момент времени , необходимо пересечение предела: учитываются короткие периоды длины , пройденные расстояния и связанные с ними средние скорости . Если позволить временному интервалу сходиться к нулю и если средние скорости также приближаются к фиксированному значению , то это значение называется (мгновенной) скоростью в данный момент времени . Описывает положение тела во время , то один пишет и имена деривационного из . ${\ Displaystyle v (т)}$${\ displaystyle t}$${\ displaystyle \ Delta t}$${\ displaystyle \ Delta x}$${\ Displaystyle {\ tfrac {\ Delta x} {\ Delta t}}}$${\ displaystyle \ Delta t}$${\ Displaystyle v (т)}$${\ displaystyle t}$${\ Displaystyle х (т)}$${\ displaystyle t}$${\ Displaystyle v (т) = х '(т)}$${\ displaystyle v}$${\ displaystyle x}$

Решающим шагом в направлении моделей дифференциальных уравнений теперь является противоположный вопрос: в примере движущегося тела скорость всегда известна, и ее положение должно быть определено на ее основе. Совершенно очевидно, что исходное положение тела также должно быть известно в определенный момент времени , чтобы иметь возможность четко решить эту проблему. Это функция от поиска , что начальное условие с заданными значениями и выполнены. ${\ displaystyle t}$${\ Displaystyle v (т)}$${\ Displaystyle х (т)}$${\ displaystyle t_ {0}}$${\ Displaystyle х (т)}$${\ Displaystyle х '(т) = v (т)}$${\ Displaystyle х (т_ {0}) = х_ {0}}$${\ displaystyle t_ {0}}$${\ displaystyle x_ {0}}$

В примере определения положения тела по его скорости явно дается вывод искомой функции. Однако обычно существует важный общий случай обыкновенных дифференциальных уравнений для требуемой величины : на основе законов природы или допущений модели известно функциональное соотношение, которое указывает, как вывод определяемой функции может быть вычислен из и от (неизвестного) значения . Кроме того, снова должно быть начальное условие, которое может быть получено, например, путем измерения требуемой переменной в фиксированный момент времени. Таким образом, мы имеем следующий общий тип проблемы: найти функцию , содержащую уравнения ${\ displaystyle x}$${\ displaystyle y}$${\ Displaystyle у '(т)}$${\ displaystyle t}$${\ Displaystyle у (т)}$${\ displaystyle y}$

${\ Displaystyle у '(т) = е (т, у (т)), \ четырехъядерный у (т_ {0}) = у_ {0}}$

где - заданная функция. ${\ displaystyle f}$

Представленное решение дифференциального уравнения аттрактора Лоренца представляет собой очень сложную кривую в трехмерном пространстве.

Простой пример - размер, который растет в геометрической прогрессии . Это означает, что текущее изменение, т.е. производная, пропорционально самому себе. То же самое касается скорости роста и, например, начального состояния . В этом случае искомое решение уже может быть найдено с помощью элементарного дифференциального исчисления и определено с помощью экспоненциальной функции : Она применима . ${\ displaystyle y}$${\ Displaystyle у '(т)}$ ${\ Displaystyle у (т)}$${\ Displaystyle у '(т) = \ лямбда у (т)}$${\ displaystyle \ lambda}$${\ Displaystyle у (0) = у_ {0}}$${\ displaystyle y}$${\ Displaystyle у (т) = у_ {0} е ^ {\ лямбда т}}$

Функция искала в дифференциальном уравнении может быть вектор- , то есть, для каждого есть может быть вектор с компонентами. Тогда говорят о -мерной системе дифференциальных уравнений. В случае движущегося тела, его положение в n - мерном евклидовом пространстве и его скорость затем в то время . Таким образом, дифференциальное уравнение определяет скорость искомой траектории с указанием направления и величины в каждой точке времени и пространства . Исходя из этого, следует рассчитать сам путь. ${\ displaystyle y}$${\ displaystyle t}$${\ Displaystyle у (т) = (у_ {1} (т), \ dotsc, у_ {д} (т))}$${\ displaystyle d}$${\ displaystyle d}$${\ Displaystyle у (т)}$${\ displaystyle d}$${\ Displaystyle у '(т)}$${\ displaystyle t}$

Основная идея одноэтапного процесса

Используя простое дифференциальное уравнение экспоненциального роста, рассмотренное в качестве примера выше, функция решения может быть указана напрямую. В общем, это невозможно с более сложными проблемами. Затем при определенных дополнительных условиях можно показать для функции, что существует однозначно определенное решение задачи начального значения; Однако это больше не может быть вычислено явно с использованием методов анализа (таких как разделение переменных , экспоненциальный подход или вариация констант ). В этом случае можно использовать численные методы для аппроксимации искомого решения. ${\ displaystyle f}$

Методы численного решения начальных задач обыкновенных дифференциальных уравнений можно условно разделить на две большие группы: одношаговый и многошаговый. Обе группы объединяет то, что они постепенно вычисляют приближения для желаемых значений функции в точках . Определяющим свойством одношагового метода является то, что для определения следующего приближения используется только «текущее» приближение . В отличие от этого, в случае многоступенчатых методов также включаются предварительно рассчитанные приближения; поэтому трехэтапный метод , например, также будет использовать и для определения нового приближения . ${\ displaystyle y_ {0}, y_ {1}, y_ {2}, \ dotsc}$${\ Displaystyle у (т_ {0}), у (т_ {1}), у (т_ {2}), \ dotsc}$${\ Displaystyle т_ {0} <т_ {1} <т_ {2} <\ ldots}$${\ displaystyle y_ {j + 1}}$${\ displaystyle y_ {j}}$${\ displaystyle y_ {j}}$${\ displaystyle y_ {j-1}}$${\ displaystyle y_ {j-2}}$${\ displaystyle y_ {j + 1}}$

Два шага явного метода Эйлера

Самый простой и самый простой одношаговый метод - это явный метод Эйлера , который швейцарский математик и физик Леонард Эйлер представил в своем учебнике Institutiones Calculi Integralis в 1768 году . Идея этого метода состоит в том, чтобы аппроксимировать искомое решение кусочно-линейной функцией, в которой наклон прямой задается на каждом шаге от точки к точке . Точнее: задача уже дает значение искомой функции, а именно . Но вывод на этом этапе также известен, потому что он применим . Таким образом, можно определить касательную к графику функции решения и использовать ее в качестве приближения. На данный момент есть размер шага${\ displaystyle t_ {j}}$${\ displaystyle t_ {j + 1}}$${\ displaystyle f (t_ {j}, y_ {j})}$${\ Displaystyle у (т_ {0}) = у_ {0}}$${\ displaystyle y '(t_ {0}) = f (t_ {0}, y_ {0})}$${\ displaystyle t_ {1}> t_ {0}}$${\ displaystyle h_ {0}: = t_ {1} -t_ {0}}$

${\ displaystyle y (t_ {1}) \ приблизительно y_ {0} + h_ {0} f (t_ {0}, y_ {0}) =: y_ {1}}$.

Теперь эту процедуру можно продолжить, выполнив следующие шаги. В целом это приводит к правилу вычисления для явного метода Эйлера

${\ displaystyle y_ {j + 1} = y_ {j} + h_ {j} f (t_ {j}, y_ {j}), \ quad j = 0,1,2, \ dotsc}$

с размерами шага .${\ displaystyle h_ {j} = t_ {j + 1} -t_ {j}}$

Явный метод Эйлера является отправной точкой для многочисленных обобщений, в которых наклон заменен наклонами, которые приближают поведение решения между точками и более точно. Неявный метод Эйлера, который используется в качестве наклона, дает дополнительную идею для одношаговых методов . На первый взгляд этот выбор не кажется подходящим, так как он неизвестен. Уравнение теперь получено как шаг процедуры. ${\ displaystyle f (t_ {j}, y_ {j})}$${\ displaystyle t_ {j}}$${\ displaystyle t_ {j + 1}}$${\ displaystyle f (t_ {j + 1}, y_ {j + 1})}$${\ displaystyle y_ {j + 1}}$

${\ displaystyle y_ {j + 1} = y_ {j} + h_ {j} f (t_ {j + 1}, y_ {j + 1})}$

из которых (при необходимости численным методом) можно рассчитать. Если, например, в качестве наклона выбрано среднее арифметическое наклонов явного и неявного метода Эйлера, получается неявный метод трапеций . Из этого можно получить явный метод, например, если аппроксимировать неизвестное в правой части уравнения путем аппроксимации явным методом Эйлера, так называемым методом Гойна . Все эти процедуры и все другие обобщения имеют общую общую идею одноэтапной процедуры: шаг ${\ displaystyle y_ {j + 1}}$${\ displaystyle y_ {j + 1}}$

${\ displaystyle y_ {j + 1} = y_ {j} + h_ {j} \ Phi}$

с наклоном , который может зависеть от , и и (в случае неявных методов) на. ${\ displaystyle \ Phi}$${\ displaystyle t_ {j}}$${\ displaystyle y_ {j}}$${\ displaystyle h_ {j}}$${\ displaystyle y_ {j + 1}}$

определение

С учетом соображений, приведенных во вводном разделе этой статьи, концепцию одношаговой процедуры можно определить следующим образом: мы ищем решение проблемы начального значения. ${\ displaystyle y}$

${\ Displaystyle у '(т) = е (т, у (т))}$, .${\ displaystyle \ quad y (t_ {0}) = y_ {0}}$

Предполагается, что решение

${\ Displaystyle у \ двоеточие I \ в \ mathbb {R} ^ {d}}$

существует на заданном интервале и определяется однозначно. находятся ${\ displaystyle I = [t_ {0}, T]}$

${\ displaystyle t_ {0} <t_ {1} <t_ {2} <\ ldots <t_ {n} = T}$

Промежуточные точки в интервале и соответствующие размеры шагов, то это означает, что через ${\ displaystyle I}$${\ displaystyle h_ {j} = t_ {j + 1} -t_ {j}}$

${\ displaystyle y_ {j + 1} = y_ {j} + h_ {j} \ Phi (t_ {j}, y_ {j}, y_ {j + 1}, h_ {j})}$, ${\ displaystyle \ quad j = 0, \ dotsc, n-1}$

Данные процедуры одношаговая процедура с функцией процедуры . Если это не зависит от, то это называется явной одношаговой процедурой . В противном случае уравнение для должно решаться на каждом шаге, и процедура называется неявной .${\ displaystyle \ Phi}$${\ displaystyle \ Phi}$${\ displaystyle y_ {j + 1}}$${\ displaystyle j}$${\ displaystyle y_ {j + 1}}$

Последовательность и конвергенция

Порядок сходимости

Глобальная ошибка при разных размерах шага для трех одношаговых методов. На графике с двойным логарифмом зависимость выглядит приблизительно линейной, наклоны соответствуют порядкам сходимости 1, 2 и 4.${\ displaystyle h}$

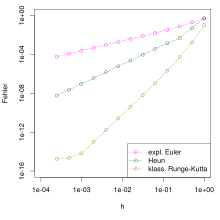
Для практического одношагового метода, рассчитанные хорошие приближения для значений точного решения должны быть в точке . Поскольку величины обычно являются -мерными векторами, качество этого приближения измеряется с помощью векторной нормы как , погрешность в точке . Желательно, чтобы эти ошибки быстро сходились к нулю для всех, если разрешено схождение размеров шага к нулю. Чтобы также охватить случай непостоянных размеров шага, его более точно определяют как максимум из используемых размеров шага и рассматривают поведение максимальной ошибки во всех точках по сравнению со степенями . Говорят, что одношаговая процедура решения заданной начальной задачи имеет порядок сходимости, если оценка ${\ displaystyle y_ {j}}$${\ displaystyle y (t_ {j})}$${\ displaystyle y}$${\ displaystyle t_ {j}}$${\ displaystyle d}$${\ Displaystyle \ | y_ {j} -y (t_ {j}) \ |}$${\ displaystyle t_ {j}}$${\ displaystyle j}$${\ displaystyle h}$${\ displaystyle t_ {j}}$${\ displaystyle h}$ ${\ displaystyle p \ geq 1}$

${\ displaystyle \ max _ {j = 0, \ dotsc, n} \ | y_ {j} -y (t_ {j}) \ | \ leq Ch ^ {p}}$

выполняется для всех достаточно малых с постоянной, не зависящей от .${\ displaystyle h}$${\ displaystyle h}$${\ displaystyle C> 0}$

Порядок сходимости - самый важный параметр для сравнения различных одношаговых процедур. Метод с более высоким порядком сходимости обычно обеспечивает меньшую общую ошибку для заданного размера шага или, наоборот, требуется меньшее количество шагов для достижения заданной точности. В случае метода с, следует ожидать, что если размер шага будет уменьшен вдвое, ошибка будет уменьшена только примерно вдвое. Однако в случае метода порядка сходимости можно предположить, что ошибка уменьшается примерно в раз . ${\ displaystyle p}$${\ displaystyle p = 1}$${\ displaystyle p = 4}$${\ Displaystyle {\ bigl (} {\ tfrac {1} {2}} {\ bigr)} ^ {4} = {\ tfrac {1} {16}}}$

Глобальная и локальная ошибка

Ошибки, учитываемые при определении порядка сходимости , состоят из двух отдельных компонентов, что поначалу кажется сложным: конечно, они зависят, с одной стороны, от ошибки, которую процедура делает на одном этапе, в том смысле, что неизвестный наклон искомой функции заменяется приближением процедурной функции. С другой стороны, необходимо также учитывать, что начальная точка шага обычно еще не совпадает с точной начальной точкой ; ошибка после этого шага также зависит от всех ошибок, которые уже были сделаны на предыдущих шагах. Из-за единообразного определения одношаговой процедуры, которая отличается только выбором процедурной функции , можно доказать, что (при определенных технических условиях ) можно вывести порядок сходимости непосредственно из порядка ошибки за один шаг, так называемый порядок согласованности . ${\ Displaystyle \ | y_ {j} -y (t_ {j}) \ |}$${\ displaystyle (t_ {j}, y_ {j})}$${\ displaystyle (t_ {j}, y (t_ {j}))}$${\ displaystyle \ Phi}$${\ displaystyle \ Phi}$

Концепция согласованности - это общее и центральное понятие в современной вычислительной математике. Исследуя, насколько хорошо численные приближения соответствуют точному решению во время сходимости процедуры, когда дело доходит до согласованности, попросту говоря, задается «противоположный» вопрос: насколько хорошо точное решение соответствует процедурной спецификации? В этой общей теории считается, что метод сходится тогда и только тогда, когда он непротиворечив и устойчив . Чтобы упростить обозначения, при следующем рассмотрении следует предположить, что явная одношаговая процедура

${\ displaystyle y_ {j + 1} = y_ {j} + h \ Phi (t_ {j}, y_ {j}, h)}$

с постоянным размером шага . Истинное решение определяет локальную ошибку отсечения (также называемую локальной процедурной ошибкой) как${\ displaystyle h}$${\ Displaystyle т \ mapsto у (т)}$${\ displaystyle \ eta}$

${\ displaystyle \ eta (t, h) = y (t) + h \ Phi (t, y (t), h) -y (t + h)}$.

Таким образом, предполагается, что точное решение известно, начинается этап процесса в этой точке и формируется разница с точным решением в этой точке . Это определяет: Одношаговая процедура имеет порядок согласованности, если оценка ${\ Displaystyle (т, у (т))}$${\ displaystyle t + h}$ ${\ displaystyle p \ geq 1}$

${\ Displaystyle \ | \ эта (т, ч) \ | \ Leq Ch ^ {p + 1}}$

выполняется для всех достаточно малых с постоянной, не зависящей от . ${\ displaystyle h}$${\ displaystyle h}$${\ displaystyle C> 0}$

Заметная разница между определениями порядка согласованности и порядка сходимости заключается в степени вместо . Это можно ясно интерпретировать таким образом, что мощность размера шага «теряется» при переходе от локальной ошибки к глобальной. Применяется следующая теорема, которая является центральной в теории одношаговой процедуры:${\ displaystyle h ^ {p + 1}}$${\ displaystyle h ^ {p}}$

Если функция процесса липшицева и соответствующий одношаговый процесс имеет порядок согласованности , то он также имеет порядок сходимости .${\ displaystyle \ Phi}$ ${\ displaystyle p}$${\ displaystyle p}$

Липшицевость функции процесса как дополнительное требование устойчивости обычно всегда выполняется, если функция из дифференциального уравнения сама липшицева. Это требование в любом случае должно соблюдаться для большинства приложений, чтобы гарантировать однозначную разрешимость проблемы начального значения. Согласно теореме достаточно определить порядок согласованности одношаговой процедуры. В принципе, это может быть достигнуто с помощью разложения в ряд Тейлора по степеням . На практике полученные формулы для высших порядков становятся очень сложными и запутанными, поэтому требуются дополнительные понятия и обозначения.${\ displaystyle f}$${\ Displaystyle \ eta (т, ч)}$${\ displaystyle h}$

Жесткость и А-устойчивость

Порядок сходимости метода - это асимптотическое утверждение, которое описывает поведение приближений, когда размер шага сходится к нулю. Однако это ничего не говорит о том, действительно ли метод вычисляет полезное приближение для заданного фиксированного размера шага. Чарльз Фрэнсис Кертисс и Джозеф О. Хиршфельдер впервые описали в 1952 году, что это может быть большой проблемой для определенных типов задач начального значения . Они заметили, что решения некоторых систем дифференциальных уравнений кинетики химических реакций не могут быть вычислены с использованием явного численными методами, и они назвали такие задачи начального значения «жесткими». Существует множество математических критериев для определения степени сложности данной проблемы. Очевидно, что жесткие задачи с начальным значением - это в основном системы дифференциальных уравнений, в которых некоторые компоненты становятся постоянными очень быстро, а другие компоненты изменяются очень медленно. Такое поведение обычно возникает при моделировании химических реакций. Наиболее полезное определение жесткости для практического применения: Задача начального значения является жесткой, если нужно выбрать размер шага «слишком малым», чтобы получить пригодное для использования решение с помощью явного одношагового метода. Такие проблемы можно решить только неявными методами.

Для вычисления экспоненциально падающего решения (синий) явный метод Эйлера (красный) совершенно бесполезен, если размер шага слишком велик; неявный метод Эйлера (зеленый) качественно правильно определяет решение для любого размера шага.

Этот эффект можно более точно проиллюстрировать, исследуя, как отдельные методы справляются с экспоненциальным затуханием . Для этого рассмотрим в тестовое уравнение в соответствии со шведским математиком Гермунд Dahlquist

${\ Displaystyle у '(т) = \ лямбда у (т), \ четырехъядерный у (0) = 1}$

с экспоненциально убывающим решением . На графике напротив показано - в качестве примера явного и неявного метода Эйлера - типичное поведение этих двух групп методов в этой, казалось бы, простой задаче начального значения: если в явном методе используется слишком большой размер шага, то сильно колеблется значения результата, которые находятся в построении расчета и перемещаются все дальше и дальше от точного решения. С другой стороны, неявные методы обычно качественно правильно вычисляют решение для любого размера шага, а именно как экспоненциально убывающую последовательность приближенных значений.${\ displaystyle \ lambda <0}$${\ Displaystyle у (т) = е ^ {\ лямбда т}}$

Вышеупомянутое тестовое уравнение также рассматривается в более общем плане для комплексных значений . В этом случае решения колебания которых амплитуда остается ограниченной , если , если это применимо, то есть реальный компонент из меньше или равно 0. Это позволяет сформулировать желаемое свойство одношаговых методов, которые должны использоваться для жестких задач начального значения: так называемую A-устойчивость. Метод называется A-стабильным, если он применяется к уравнению теста для любого размера шага и вычисляется для всех с последовательностью приближений, которая (как и истинное решение) остается ограниченной. Неявный метод Эйлера и неявный метод трапеций являются простейшими примерами A-стабильных одношаговых методов. С другой стороны, можно показать, что явная процедура никогда не может быть A-стабильной.${\ displaystyle \ lambda}$${\ Displaystyle \ OperatorName {Re} (\ лямбда) \ leq 0}$${\ displaystyle \ lambda}$${\ displaystyle h> 0}$${\ displaystyle \ lambda}$${\ Displaystyle \ OperatorName {Re} (\ лямбда) \ leq 0}$${\ displaystyle y_ {0}, y_ {1}, y_ {2}, \ dotsc}$

Специальные процедуры и классы процедур

Сравнение некоторых одноэтапных процедур

Простые процедуры порядка 1 и 2

Как французский математик Огюстен Луи Коши доказал , около 1820, метода Эйлера имеет порядок сходимости 1. Если наклоны в явном методе Эйлера и в неявном методе Эйлера , так как они существуют в двух конечных точках шага, могут быть усредненные надежды получить лучшее приближение по всему интервалу. Фактически, можно доказать, что полученный таким образом неявный трапециевидный метод${\ displaystyle f (t_ {j}, y_ {j})}$${\ displaystyle f (t_ {j + 1}, y_ {j + 1})}$

${\ displaystyle y_ {j + 1} = y_ {j} + {\ frac {h} {2}} {\ Big (} f (t_ {j}, y_ {j}) + f (t_ {j + 1 }, y_ {j + 1}) {\ Big)}}$

порядок сходимости равен 2. Этот метод имеет очень хорошие свойства устойчивости, но является неявным, так что уравнение для должно решаться на каждом шаге . Если эту величину аппроксимировать в правой части уравнения с помощью явного метода Эйлера, явный метод Хойна приведет к${\ displaystyle y_ {j + 1}}$

${\ displaystyle y_ {j + 1} = y_ {j} + {\ frac {h} {2}} {\ Big (} f (t_ {j}, y_ {j}) + f {\ big (} t_ {j + 1}, y_ {j} + hf (t_ {j}, y_ {j}) {\ big)} {\ Big)}}$,

который также имеет порядок сходимости 2. Другой простой явный метод порядка 2, улучшенный метод Эйлера , может быть получен при рассмотрении следующего: «средний» наклон на шаге процесса будет наклоном решения в середине шага, то есть в точке . Однако, поскольку решение неизвестно, оно аппроксимируется явным шагом Эйлера с половиной шага. Результаты процессуального правила ${\ displaystyle y}$${\ displaystyle t_ {j} + {\ tfrac {h} {2}}}$

${\ displaystyle y_ {j + 1} = y_ {j} + hf {\ big (} t_ {j} + {\ tfrac {h} {2}}, y_ {j} + {\ tfrac {h} {2) }} f (t_ {j}, y_ {j}) {\ big)}}$.

Все эти одношаговые методы порядка 2 были опубликованы в 1895 году немецким математиком Карлом Рунге как усовершенствования метода Эйлера .

Метод Рунге-Кутта

Классический метод Рунге-Кутты четвертого порядка усредняет четыре вспомогательных уклона (красные) на каждом шаге.

Вышеупомянутые идеи для простых одношаговых методов приводят, если они в дальнейшем обобщаются, к важному классу методов Рунге-Кутта. Например, метод Хойна можно более четко представить следующим образом: сначала вычисляется вспомогательный наклон, а именно наклон явного метода Эйлера. Здесь это определяет еще один вспомогательный наклон . Фактически используемый градиент процесса затем получается как средневзвешенное значение вспомогательных градиентов в методе Хойна . Эту процедуру можно обобщить более чем на два вспомогательных уклона. A -шаговый метод Рунге-Кутта сначала вычисляет вспомогательные градиенты , оценивая их в подходящих точках, а затем как средневзвешенное значение. В случае явного метода Рунге-Кутта вспомогательные наклоны вычисляются непосредственно один за другим; в случае неявного метода они получаются как решения системы уравнений. Типичным примером является явный, классический метод Рунге-Кутта 4 - го порядка, который иногда называют просто по методу Рунге-Кутта: Во- первых, четыре вспомогательные трассы используются ${\ displaystyle k_ {1} = f (t_ {j}, y_ {j})}$${\ displaystyle k_ {2} = f (t_ {j} + h, y_ {j} + hk_ {1})}$${\ displaystyle \ Phi}$${\ displaystyle {\ tfrac {1} {2}} k_ {1} + {\ tfrac {1} {2}} k_ {2}}$${\ displaystyle s}$${\ displaystyle k_ {1}, \ dotsc, k_ {s}}$${\ displaystyle f}$${\ displaystyle \ Phi}$${\ displaystyle k_ {1}, k_ {2}, k_ {3}, \ dotsc}$

${\ displaystyle {\ begin {align} k_ {1} & = f (t_ {j}, y_ {j}) \\ k_ {2} & = f (t_ {j} + {\ tfrac {h} {2) }}, y_ {j} + {\ tfrac {h} {2}} k_ {1}) \\ k_ {3} & = f (t_ {j} + {\ tfrac {h} {2}}, y_ {j} + {\ tfrac {h} {2}} k_ {2}) \\ k_ {4} & = f (t_ {j} + h, y_ {j} + hk_ {3}) \ end {выровнено }}}$

а затем средневзвешенное значение как наклон процесса

${\ displaystyle {\ tfrac {1} {6}} k_ {1} + {\ tfrac {1} {3}} k_ {2} + {\ tfrac {1} {3}} k_ {3} + {\ tfrac {1} {6}} k_ {4}}$

использовал. Этот хорошо известный метод был опубликован немецким математиком Вильгельмом Куттой в 1901 году после того, как Карл Хойн обнаружил трехшаговый одношаговый метод порядка 3 годом ранее .

Построение явных процессов еще более высокого порядка с минимально возможным числом этапов - математически очень сложная задача. Как Джон С. Батчер смог показать в 1965 году, существует, например, только минимум шестиэтапных процедур для порядка 5; явный метод Рунге-Кутты 8-го порядка требует не менее 11 шагов. В 1978 году австрийский математик Эрнст Хайрер нашел процедуру порядка 10 с 17 шагами. Коэффициенты для такой процедуры должны удовлетворять 1205 определяющим уравнениям. В случае неявных методов Рунге-Кутта ситуация проще и яснее: для каждого количества этапов существует метод порядка ; это в то же время максимально достижимый порядок.${\ displaystyle s}$${\ displaystyle p = 2s}$

Метод экстраполяции

Идея экстраполяции не ограничивается решением задач начального значения с помощью одношаговых методов, но может применяться аналогично ко всем численным методам, которые дискретизируют решаемую задачу с шагом . Хорошо известным примером метода экстраполяции является интегрирование Ромберга для численного вычисления интегралов. В общем, пусть поэтому будет значением, которое должно быть определено численно, в случае этой статьи, например, значение функции решения задачи с начальным значением в данной точке. Численный метод, например одношаговый метод, вычисляет для этого приблизительное значение , которое зависит от выбора размера шага . Здесь предполагается, что метод сходится, т. Е. Что против, если сходится, сходится к нулю. Эта сходимость, однако, является чисто теоретическим утверждением, поскольку в реальном применении метода приблизительные значения могут быть рассчитаны для конечного числа различных размеров шага , но, конечно, вы не можете позволить размеру шага «сходиться к нулю». Вычисленные приближения для разных размеров шага, однако, можно понимать как информацию о (неизвестной) функции : в методе экстраполяции в качестве приближения используется интерполяционный полином, т.е. полином с ${\ displaystyle h}$${\ displaystyle v}$${\ Displaystyle {\ тильда {v}} (ч)}$${\ displaystyle h> 0}$${\ Displaystyle {\ тильда {v}} (ч)}$${\ displaystyle v}$${\ displaystyle h}$${\ displaystyle {\ tilde {v}} (h_ {1}), {\ tilde {v}} (h_ {2}), \ dotsc, {\ tilde {v}} (h_ {m})}$${\ displaystyle h_ {1}> h_ {2}> \ ldots> h_ {m}}$${\ Displaystyle {\ тильда {v}}}$${\ Displaystyle {\ тильда {v}}}$${\ displaystyle P}$

${\ Displaystyle P (h_ {k}) = {\ тильда {v}} (h_ {k})}$

для . Значение полинома в точке затем используется в качестве вычисляемого приближения для невычисляемого предела for в сторону нуля. Роланд Булирш и Йозеф Стоер опубликовали ранний успешный алгоритм экстраполяции для задач с начальным значением в 1966 году.${\ Displaystyle к = 1,2, \ dotsc, m}$${\ Displaystyle P (0)}$${\ displaystyle h = 0}$${\ Displaystyle {\ тильда {v}} (ч)}$${\ displaystyle h}$

Экстраполяция в порядке порядка${\ displaystyle h = 0}$${\ displaystyle p = 2}$

Конкретный пример в случае одноэтапного метода заказа может сделать понятной общую процедуру экстраполяции. С помощью такого метода вычисленное приближение для малых размеров шага можно легко преобразовать в полином вида ${\ displaystyle p}$${\ displaystyle h}$

${\ displaystyle P (h) = a + bh ^ {p}}$

с изначально неизвестными параметрами и приблизительными. Если теперь использовать процедуру для вычисления двух приближений и для одного размера шага и для половины размера шага , он получит из условий интерполяции и двух линейных уравнений для неизвестных и . Значение экстраполированы ${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle h_ {1}}$${\ displaystyle h_ {2} = {\ tfrac {1} {2}} h_ {1}}$${\ displaystyle y_ {h_ {1}}}$${\ displaystyle y_ {h_ {2}}}$${\ displaystyle P (h_ {1}) = y_ {h_ {1}}}$${\ displaystyle P (h_ {2}) = y_ {h_ {2}}}$${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle h = 0}$

${\ displaystyle P (0) = a = y_ {h_ {2}} + {\ frac {y_ {h_ {2}} - y_ {h_ {1}}} {2 ^ {p} -1}}}$

то обычно представляет собой гораздо лучшее приближение, чем два первоначально рассчитанных значения. Можно показать, что порядок одноэтапного процесса, полученного таким образом, по крайней мере , то есть по крайней мере на 1 больше, чем в исходном процессе.${\ displaystyle p + 1}$

Процедура с контролем размера шага

Одним из преимуществ одношагового метода является то, что на каждом шаге можно использовать любой размер шага независимо от других шагов . На практике это, очевидно, поднимает вопрос о том, как выбрать . В реальных приложениях всегда будет допустимая погрешность, с которой должно быть вычислено решение задачи начального значения; Например, было бы бессмысленно определять численное приближение, которое значительно «точнее», чем данные с ошибками измерения для начальных значений и параметров данной задачи. Таким образом, цель будет заключаться в выборе размеров шага таким образом, чтобы, с одной стороны, соблюдались указанные допуски ошибок, но с другой стороны, чтобы использовать как можно меньше шагов, чтобы сохранить малыми вычислительные усилия. В общем, это может быть достигнуто только в том случае, если размеры шага адаптированы к ходу решения: маленькие шаги, когда решение значительно меняется, большие шаги, когда оно почти постоянно.${\ displaystyle j}$${\ displaystyle h_ {j}}$ ${\ displaystyle h_ {j}}$

В случае хорошо обусловленных задач начального значения можно показать, что глобальная процедурная ошибка приблизительно равна сумме локальных ошибок усечения на отдельных этапах. Следовательно, следует выбирать как можно больший размер шага, который ниже выбранного порогового значения допуска. Проблема здесь в том, что он не может быть вычислен напрямую, так как он зависит от неизвестного точного решения начальной задачи в точке . Таким образом, основная идея управления размером шага состоит в приближении с помощью более точного метода, чем базовый метод, на котором он основан.${\ displaystyle \ eta _ {j}: = \ | \ eta (t_ {j}, h_ {j}) \ |}$${\ displaystyle h_ {j}}$${\ displaystyle \ eta _ {j}}$${\ displaystyle \ eta _ {j}}$${\ displaystyle y (t_ {j})}$${\ displaystyle t_ {j}}$${\ displaystyle y (t_ {j})}$

Две основные идеи для управления размером шага - это уменьшение вдвое размера шага и встроенные процедуры . При уменьшении размера шага вдвое результат для двух шагов с половинным размером шага вычисляется как сравнительное значение в дополнение к фактическому шагу процесса. Затем на основе обоих значений путем экстраполяции определяется более точное приближение для , и таким образом оценивается локальная ошибка . Если он слишком велик, этот шаг отбрасывается и повторяется с меньшим размером шага. Если он значительно меньше указанного допуска, размер шага можно увеличить на следующем шаге. Дополнительные вычислительные затраты для этого метода уменьшения вдвое размера шага относительно велики; поэтому современные реализации в основном используют так называемые встроенные методы для управления размером шага. Основная идея состоит в том, чтобы вычислить два приближения для каждого шага, используя два одношаговых метода, которые имеют разные порядки сходимости, и, таким образом, оценить локальную ошибку. Чтобы оптимизировать вычислительные усилия, две процедуры должны иметь как можно больше общих вычислительных шагов: они должны быть «встроены друг в друга». Например, встроенные методы Рунге-Кутты используют одни и те же вспомогательные наклоны и различаются только их усреднением. Хорошо известные встроенные методы включают методы Рунге-Кутта-Фельберга ( Эрвин Фельберг , 1969) и методы Дорманда-Принса (Дж. Р. Дорман и П. Дж. Принс, 1980).${\ displaystyle y (t_ {j})}$${\ displaystyle \ eta _ {j}}$${\ displaystyle y (t_ {j})}$

Практический пример: решение задач начального значения с помощью числового программного обеспечения

Для математических концепций, представленных в обзоре в этой статье, были разработаны многочисленные программные реализации, которые позволяют пользователю простым способом численно решать практические задачи. В качестве конкретного примера, решение уравнений Лотки-Вольтерра должно быть вычислено с помощью широко используемого программного обеспечения для численных расчетов Matlab . Уравнения Лотки-Вольтерры - это простая модель из биологии, которая описывает взаимодействия между популяциями хищников и жертв . Для этого дана система дифференциальных уравнений

${\ displaystyle {\ begin {align} y_ {1} '(t) & = ay_ {1} (t) -by_ {1} (t) y_ {2} (t) \\ y_ {2}' (t ) & = cy_ {1} (t) y_ {2} (t) -dy_ {2} (t) \ конец {выровнено}}}$

с параметрами и начальным условием , . Здесь и соответствуют временному развитию популяции жертвы или хищника. Решение следует рассчитывать на временном интервале . ${\ displaystyle a = 1, b = 2, c = 1, d = 1}$${\ displaystyle y_ {1} (0) = 3}$${\ displaystyle y_ {2} (0) = 1}$${\ displaystyle y_ {1}}$${\ displaystyle y_ {2}}$${\ displaystyle [0.20]}$

Для расчета с использованием Matlab сначала определяется функция в правой части дифференциального уравнения для заданных значений параметров : ${\ displaystyle f}$${\ Displaystyle у '= е (т, у)}$

a = 1; b = 2; c = 1; d = 1;
f = @(t,y) [a*y(1) - b*y(1)*y(2); c*y(1)*y(2) - d*y(2)];

Кроме того, требуется временной интервал и начальные значения:

t_int = [0, 20];
y0 = [3; 1];

Тогда решение можно рассчитать:

[t, y] = ode45(f, t_int, y0);

Функция Matlab ode45реализует одношаговый метод, который использует два встроенных явных метода Рунге-Кутта с порядками сходимости 4 и 5 для управления размером шага.

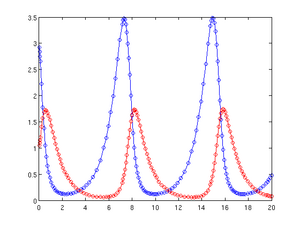
Теперь решение можно нарисовать в виде синей кривой и красной кривой ; расчетные точки отмечены маленькими кружками: ${\ displaystyle y_ {1}}$${\ displaystyle y_ {2}}$

figure(1)
plot(t, y(:,1), 'b-o', t, y(:,2), 'r-o')

Результат показан ниже на картинке слева. На правом рисунке показаны размеры шагов, используемых в процессе, которые были созданы с помощью

figure(2)
plot(t(1:end-1), diff(t))

Решения уравнений Лотки-Вольтерра.

Используемые приращения

Этот пример также может быть выполнен без изменений с помощью бесплатного программного обеспечения для вычислений GNU Octave . Однако в реализованном там методе существует несколько иная последовательность размеров шага.

литература

• Джон С. Бутчер : Численные методы для обыкновенных дифференциальных уравнений . Джон Вили и сыновья, Чичестер 2008, ISBN 978-0-470-72335-7 . 
• Вольфганг Дамен , Арнольд Реускен: Числа для инженеров и естествоиспытателей . 2-е издание. Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-76492-2 , гл. 11: Обыкновенные дифференциальные уравнения . 
• Питер Деуфлхард , Фолькмар Борнеманн : Численная математика 2 - Обыкновенные дифференциальные уравнения . 3. Издание. Вальтер де Грюйтер, Берлин 2008 г., ISBN 978-3-11-020356-1 . 
• Дэвид Ф. Гриффитс, Десмонд Дж. Хайэм: численные методы для обыкновенных дифференциальных уравнений - задачи с начальным значением . Springer, Лондон, 2010 г., ISBN 978-0-85729-147-9 . 
• Роберт Платон: Компактная вычислительная математика . 4-е издание. Vieweg + Teubner, Висбаден 2010, ISBN 978-3-8348-1018-2 , гл. 7: Одноэтапная процедура для проблем с начальным значением . 
• Ханс-Юрген Рейнхардт: Числа обыкновенных дифференциальных уравнений . 2-е издание. Вальтер де Грюйтер, Берлин / Бостон 2012, ISBN 978-3-11-028045-6 . 
• Ганс Рудольф Шварц, Норберт Кёклер: Численная математика . 8-е издание. Vieweg + Teubner, Висбаден 2011, ISBN 978-3-8348-1551-4 , гл. 8: проблемы начального значения . 
• Карл Штрехмель, Рюдигер Вайнер, Гельмут Подхайский: Числа обыкновенных дифференциальных уравнений . 2-е издание. Springer Spectrum, Висбаден 2012 г., ISBN 978-3-8348-1847-8 . 

веб ссылки

• Ларс Грюне: Численные методы для обыкновенных дифференциальных уравнений (Численная математика II). (PDF) 2008, по состоянию на 20 августа 2018 г. (конспекты лекций Университета Байройта ). 
• Питер Спеллуччи: Числа обыкновенных дифференциальных уравнений. (PDF) 2007, по состоянию на 20 августа 2018 г. (конспекты лекций Технического университета Дармштадта ). 
• Ханс У. Фукс: Численные методы для дифференциальных уравнений. (PDF) 2007, по состоянию на 20 августа 2018 г. (английский, лекции Цюрихского университета прикладных наук ). 
• Учебник по математике: калькулятор общих дифференциальных уравнений первого порядка. В: Учебник по математике. Проверено 20 августа 2018 года . 

Индивидуальные доказательства

1. ^ Томас Сонар : 3000 лет анализа . Springer, Берлин / Гейдельберг 2011, ISBN 978-3-642-17203-8 , стр. 378-388 и 401-426 . 
2. ↑ Жан-Люк Шаберт и др.: История алгоритмов . Springer, Berlin / Heidelberg 1999, ISBN 978-3-540-63369-3 , стр. 374-378 . 
3. ↑ Вольфганг Дамен, Арнольд Реускен: Численный анализ для инженеров и ученых . 2-е издание. Springer, Берлин / Гейдельберг, 2008 г., ISBN 978-3-540-76492-2 , стр. 386 f . 
4. ↑ Вольфганг Дамен, Арнольд Реускен: Численный анализ для инженеров и ученых . 2-е издание. Springer, Берлин / Гейдельберг, 2008 г., ISBN 978-3-540-76492-2 , стр. 386-392 . 
5. ↑ Ханс Рудольф Шварц, Норберт Кёклер: Численная математика . 8-е издание. Vieweg + Teubner, Висбаден 2011, ISBN 978-3-8348-1551-4 , стр. 350 f . 
6. ^ Роберт Платон: Компактная вычислительная математика . 4-е издание. Vieweg + Teubner, Висбаден 2010, ISBN 978-3-8348-1018-2 , стр. 157 . 
7. ^ Роберт Платон: Компактная вычислительная математика . 4-е издание. Vieweg + Teubner, Висбаден 2010, ISBN 978-3-8348-1018-2 , стр. 156 . 
8. ^ Роберт Платон: Компактная вычислительная математика . 4-е издание. Vieweg + Teubner, Висбаден 2010, ISBN 978-3-8348-1018-2 , стр. 157 . 
9. ↑ Ханс-Юрген Рейнхардт: Числа обыкновенных дифференциальных уравнений . 2-е издание. Вальтер де Грюйтер, Берлин / Бостон 2012, ISBN 978-3-11-028045-6 , стр. 42 f . 
10. ^ Джон С. Бутчер: Численные методы для обыкновенных дифференциальных уравнений . John Wiley & Sons, Чичестер, 2008 г., ISBN 978-0-470-72335-7 , стр. 95-100 . 
11. ^ JC Butcher: Численные методы для обыкновенных дифференциальных уравнений в 20 веке . В кн . : Журнал вычислительной и прикладной математики . Лента 125 , нет. 1-2 , 15 декабря 2000 г., стр. 21 год f . ( онлайн ). 
12. ↑ Питер Деуфлхард, Фолькмар Борнеманн: Численная математика 2 - Обыкновенные дифференциальные уравнения . 3. Издание. Вальтер де Грюйтер, Берлин, 2008 г., ISBN 978-3-11-020356-1 , стр. 228 f . 
13. ↑ Питер Деуфлхард, Фолькмар Борнеманн: Численная математика 2 - Обыкновенные дифференциальные уравнения . 3. Издание. Вальтер де Грюйтер, Берлин, 2008 г., ISBN 978-3-11-020356-1 , стр. 229-231 . 
14. ↑ Вольфганг Дамен, Арнольд Реускен: Численный анализ для инженеров и ученых . 2-е издание. Springer, Берлин / Гейдельберг, 2008 г., ISBN 978-3-540-76492-2 , стр. 443 f . 
15. ^ Карл Штрехмель, Рюдигер Вайнер, Гельмут Подхайский: Числа обыкновенных дифференциальных уравнений . 2-е издание. Springer Spectrum, Висбаден 2012, ISBN 978-3-8348-1847-8 , стр. 258 f . 
16. ↑ Жан-Люк Шаберт и др.: История алгоритмов . Springer, Berlin / Heidelberg 1999, ISBN 978-3-540-63369-3 , стр. 378 f . 
17. ↑ Жан-Люк Шаберт и др.: История алгоритмов . Springer, Berlin / Heidelberg 1999, ISBN 978-3-540-63369-3 , стр. 381-388 . 
18. ↑ Вольфганг Дамен, Арнольд Реускен: Численный анализ для инженеров и ученых . 2-е издание. Springer, Берлин / Гейдельберг, 2008 г., ISBN 978-3-540-76492-2 , стр. 406 f . 
19. ^ JC Butcher: Численные методы для обыкновенных дифференциальных уравнений в 20 веке . В кн . : Журнал вычислительной и прикладной математики . Лента 125 , нет. 1-2 , 15 декабря 2000 г., стр. 4-6 ( онлайн ). 
20. ↑ Питер Деуфлхард, Фолькмар Борнеманн: Численная математика 2 - Обыкновенные дифференциальные уравнения . 3. Издание. Вальтер де Грюйтер, Берлин, 2008 г., ISBN 978-3-11-020356-1 , стр. 160-162 . 
21. ^ Карл Штрехмель, Рюдигер Вайнер, Гельмут Подхайский: Числа обыкновенных дифференциальных уравнений . 2-е издание. Springer Spectrum, Висбаден 2012, ISBN 978-3-8348-1847-8 , стр. 219-221 . 
22. ^ Карл Штрехмель, Рюдигер Вайнер, Гельмут Подхайский: Числа обыкновенных дифференциальных уравнений . 2-е издание. Springer Spectrum, Висбаден 2012, ISBN 978-3-8348-1847-8 , стр. 79 ff . 
23. ^ JC Butcher: Численные методы для обыкновенных дифференциальных уравнений в 20 веке . В кн . : Журнал вычислительной и прикладной математики . Лента 125 , нет. 1-2 , 15 декабря 2000 г., стр. 26 ( онлайн ). 
24. ^ Роберт Платон: Компактная вычислительная математика . 4-е издание. Vieweg + Teubner, Висбаден 2010, ISBN 978-3-8348-1018-2 , стр. 171-173 . 
25. ^ Карл Штрехмель, Рюдигер Вайнер, Гельмут Подхайский: Числа обыкновенных дифференциальных уравнений . 2-е издание. Springer Spectrum, Висбаден 2012, ISBN 978-3-8348-1847-8 , стр. 57-59 . 
26. ↑ Питер Деуфлхард, Фолькмар Борнеманн: Численная математика 2 - Обыкновенные дифференциальные уравнения . 3. Издание. Вальтер де Грюйтер, Берлин, 2008 г., ISBN 978-3-11-020356-1 , стр. 199-204 . 
27. ^ Роберт Платон: Компактная вычислительная математика . 4-е издание. Vieweg + Teubner, Висбаден 2010, ISBN 978-3-8348-1018-2 , гл. 7: Одношаговый метод решения задач с начальным значением , стр. 173-177 . 
28. ^ Карл Штрехмель, Рюдигер Вайнер, Гельмут Подхайский: Числа обыкновенных дифференциальных уравнений . 2-е издание. Springer Spectrum, Висбаден 2012, ISBN 978-3-8348-1847-8 , стр. 64-70 . 
29. ↑ ode45: Решите нежесткие дифференциальные уравнения - метод среднего порядка. MathWorks, доступ к 23 ноября 2017 .