Экзистенциальные графы

Экзистенциальные графы (немецкие переводы «экзистенциальные графы» и «графы существования» не очень распространены) - это логическая система американского логика и философа Чарльза Сандерса Пирса . Они включают как свои собственные графические обозначения для логических утверждений, так и логическое исчисление , т. Е. ЧАС. (по сути) формальная система правил вывода, с помощью которой существующие утверждения могут быть преобразованы таким образом, что новые утверждения возникают из первых.

введение

Пирс счел алгебраическую нотацию (то есть формульную нотацию) логики, особенно логику предикатов , которая была очень новой при его жизни и которую он сам помогал развить, философски неудовлетворительной, потому что символическим символам придавалось их значение посредством простой условности. Напротив, он стремился к нотации, в которой персонажи воспринимают свое значение буквально в себе - в терминологии его теории знаков : система знаковых персонажей, которые подобны упомянутым объектам и отношениям или одинаковы.

Разработка знаковой, графической и, как он задумал, интуитивно понятной и легко обучаемой логической системы была проектом, который занимал Пирса всю его жизнь. После, по крайней мере, одного прекращенного подхода - «сущностных графов» - с 1896 года, наконец, была создана закрытая система экзистенциальных графов. Хотя их создатель считал их явно превосходящей и более интуитивной системой, они, как запись и как исчисление, мало влияли на историю логики; Это объясняется, с одной стороны, тем фактом, что Пирс опубликовал очень мало по этой теме, а опубликованные тексты были написаны не очень четко; и, с другой стороны, тот факт, что запись линейных формул в руках экспертов является менее трудоемким инструментом. Графам существования уделялось мало внимания или они рассматривались как громоздкие обозначения.

С 1963 года работы Дона Д. Робертса и Дж. Джея Земана, в которых графические системы Пирса были систематически исследованы и представлены, привели к лучшему пониманию. Однако сегодня практическую роль играет только современное приложение - графы понятий, введенные Джоном Ф. Сова в 1976 году , которые используются в информатике для представления знаний . В качестве темы исследования экзистенциальные графы все чаще появляются снова в связи с растущим интересом к графической логике, который также выражается в попытках заменить правила вывода, данные Пирсом, более интуитивными.

Общая система экзистенциальных графов состоит из трех подсистем, которые строятся друг на друге: альфографов, бета-графиков и гаммаграфов. Альфаграфы - это чисто пропозициональная система . На их основе параграфы становятся настоящим расширением, логической системой предикатов первого уровня. Гаммаграфы, которые на сегодняшний день не были полностью исследованы и не завершены Пирсом, считаются дальнейшим развитием абзацев альфа и бета. При правильной интерпретации гаммаграфы охватывают логику предикатов более высокого уровня и модальную логику . В 1903 году Пирс начал с нового подхода, «настоянных экзистенциальных графов», с помощью которых он хотел заменить предыдущие системы альфа, бета и гаммаграфов и объединить их выразительность и производительность в единой новой системе. Как и гаммаграфы, окрашенные экзистенциальные графы остались незаконченными.

Как исчисления, альфа- и бета-абзацы являются правильными (т.е. все выражения, которые могут быть выведены как альфа- или бета-абзацы, семантически действительны с точки зрения логики высказываний или предикатов ) и полными (т.е. все выражения, которые семантически допустимы в логике высказываний или предикатов, являются альфа- или абзацы могут быть производными).

Пирс обосновал выбор термина «экзистенциальные графы» тем, что в простейшем значимом и правильно сформированном абзаце содержится утверждение о существовании. Пирс впервые использовал этот термин в конце 1897 года; заранее он говорит о «положительных логических графах» или просто о своей системе логических диаграмм.

В этой статье параграфы альфа и бета рассматриваются как наиболее совершенная и наиболее изученная часть системы Пирса. Дополнительную информацию предоставляют произведения, указанные в списке литературы.

Алфавиты

Обозначение альфографов

Алфавиты

Атомарные операторы , т.е. ЧАС. Утверждения, которые не состоят из других утверждений, - как обычно в логике высказываний - выражаются буквами; например, атомарное утверждение «Идет дождь» можно выразить буквой «P». Конъюнкция нескольких операторов - атомных или неатомарных - выражается в письменной форме их рядом друг с другом. Следовательно, чтобы сказать, что два утверждения P и Q верны, пишут «PQ».

Помимо союза, система включает отрицание . Он выражается в том, что выражение, которое нужно отрицать, - независимо от того, простое оно или составное - окружено замкнутой линией, так сказать «окольцовано». Особых требований к форме линии нет, но обычно используют круг или овал. Пирс называет замкнутую строку, которая отрицает утверждение, сокращением (буквально: вырезать). Графический фон вырезки состоит в том, что утверждения, которые считаются истинными, записаны на листе бумаги, который написан на листе утверждений . Ложные утверждения должны быть исключены, разграничены, «отрезаны» от области истинных утверждений, и это как раз и является функцией сокращения.

Чтобы выразить условное , т.е. То есть, чтобы сказать, что утверждение P является достаточным условием для утверждения Q, выбирается обозначение, которое называется «P прокручивает Q», «P свертывает Q»: утверждение Q, то есть условное предложение стоит внутри своего собственного отрезка вместе со своим условием, утверждением P, во втором, внешнем отрезке (см. рисунок, точки c1 и c2). Это обозначение вводится атомарно в логической системе экзистенциальных графов, но, зная, что разрез - это отрицание, а сопоставление - это соединение, его можно легко привести в соответствие с условиями истинности этих двух связей: Условное, P → Q эквивалентно отрицанию ¬ (P ∧ ¬Q), и это в точности утверждение «P прокручивает Q», которое точно отделяет случай истинного P и ложного Q от листа утверждения , «вырезает».

Дизъюнкции выражается путем записи двух дизъюнктов - каждая по отдельности размещены в отдельных сокращений - рядом друг с другом , и добавление дополнительного внешнего разреза. Легко видеть, что это обозначение представляет собой утверждение ¬ (¬P∧¬Q) в современных обозначениях, утверждение, которое эквивалентно P∨Q. И снова наглядный фон состоит в том, что дизъюнкция исключает случай из списка утверждений, что и P, и Q ложны.

С помощью двух звеньев алфавитов, отрицание (разрез) и операции И (записывая несколько заявлений о приеме листе) - как было показан в качестве примера на условный и дизъюнкцию - все другие звенья двузначной логики может быть представлены (см функциональными Полнота столярных изделий ). Таким образом, алфавиты являются полноценным обозначением логики высказываний.

Если утверждения в написании алфавитов должны обрабатываться электронными компьютерами или просто воспроизводиться с помощью систем обработки текстов или более ранних пишущих машинок, часто приходится ограничиваться выражением сокращений с помощью скобок. Вместо того чтобы обвести предложение P замкнутой линией, напишите в этом случае (P). Условное обозначение «P прокручивает Q» в этом обозначении становится (P (Q)). Эта статья используется по типографским причинам.

Заключительные правила алфавитов

Чтобы сформулировать правила, сначала необходимо определить понятие уровня утверждения (в литературе: «уровень предложения»). Уровень - элементарного или составного - утверждения определяется как количество сокращений, которые прямо или косвенно окружают это утверждение. Например, в выражении (P (Q)) плоскости P и (Q) равны 1, потому что и P, и (Q) являются только частью внешнего разреза. Уровень Q, с другой стороны, равен 2, потому что Q не только непосредственно окружен разрезом, но и, в свою очередь, является частью внешнего разреза.

После этого предварительного замечания окончательные правила могут быть сформулированы следующим образом:

принятие

Правило предположения позволяет записать любое утверждение в качестве предпосылки и сделать из него выводы. Если вы хотите вывести аргумент, который включает более одной посылки, то вы пишете посылки рядом друг с другом - написание рядом друг с другом не означает ничего, кроме принятия каждого из предложений, объединенных таким образом.

R1 - Правило стирания

Любой оператор, который встречается на четном уровне, может быть удален без замены. С помощью этого правила можно, например, сделать вывод из (P (Q)), удалив Q до (P ()), потому что Q находится на уровне 2, а 2 - четное число. В этом примере P не следует удалять, потому что P находится на уровне 1, а 1 - нечетное число.

R2 - Правило вставки

Любой оператор может быть вставлен на нечетном уровне. Например, можно вывести (PR (Q)) из (P (Q)) с помощью этого правила: вставленный оператор R находится на уровне 1, а 1 - нечетное число.

R3 - Правило итерации

Любой оператор, который является частью составного оператора, может повторяться на том же уровне или на более низком уровне, но не внутри себя. Согласно R3, например, из (P (Q)) путем повторения P на том же уровне на (P ( Q) P) или повторением P на более низком уровне до (P (QP)). Точно так же то же утверждение можно использовать для вывода (P (Q) (Q)), повторяя (Q). Было бы недопустимо повторять (Q) внутри себя и, таким образом, делать вывод (P (Q (Q))) - эта теоретическая возможность исключена дополнительным условием, что повторение утверждения не должно производиться внутри самого себя.

R4 - Отмена повторения («Правило деитерации»)

Если утверждение X формально имеет форму, которая могла бы возникнуть из утверждения Y, применяя R3, правило повторения, то R4 может использоваться для вывода от X к Y; не обязательно, что X действительно возник в результате применения R3. Например, R4 можно использовать для вывода от (P (Q) (Q)) к (P (Q)), потому что R3 можно использовать для вывода от (P (Q)) к (P (Q) (Q)).

R5 - Правило двойного удара

Двойные разрезы могут быть вставлены и удалены по желанию как вокруг существующих операторов, так и сами по себе. Например, согласно R5, можно сделать вывод от PQ к P ((Q)), к ((P)) Q, а также к ((PQ)). Однако также можно сделать вывод от PQ к PQ (()) или к P (()) Q.

пример

Она должна быть получена из и утверждения ( звено цепи ). Для этого нужно начать с предположений (P (Q)) и (Q (R)) и постепенно получить утверждение (P (R)): ${\ displaystyle P \ rightarrow Q}$${\ Displaystyle Q \ rightarrow R}$${\ Displaystyle P \ rightarrow R}$

(P (Q)) (Q (R))	${\ displaystyle \ longrightarrow}$	(P (Q (Q (R)) )) (Q (R))	(R3)
(P (Q (Q (R)))) (Q (R))	${\ displaystyle \ longrightarrow}$	(P (Q (Q (R))))	(R1)
(P ( Q ( Q (R))))	${\ displaystyle \ longrightarrow}$	(P (Q ((R))))	(R4)
(P (Q (( R )) ))	${\ displaystyle \ longrightarrow}$	(P (QR))	(R5)
(P ( Q R))	${\ displaystyle \ longrightarrow}$	(P (R))	(R1)

Абзацы

Абзацы - это логическая система предикатов экзистенциальных графов. Они расширяют систему алфавитов лингвистическим элементом линии идентичности и обобщают уже существующие правила замыкания.

Атомарные выражения в абзацах больше не являются буквами утверждений (P, Q, R, ...) или утверждениями («Идет дождь», «Пирс умер в бедности»), а являются предикатами в смысле логики предикатов (подробности см. Там), возможно сокращенными для предикатных букв (F, G, H, ...). Предикат в смысле логики предикатов - это последовательность слов с четко определенными пробелами, которая становится утверждением, если собственное имя вставлено в каждое пробел. Например, последовательность слов «_ умер в бедности» является сказуемым, потому что предложение «Пирс умер в бедности» возникает из нее, если в поле ввести собственное имя «Пирс». Кроме того, последовательность слов «_ ₁ богаче _ ₂ » является сказуемое, потому что утверждение «Сократ богаче Платона» возникает из него , если собственные имена «Сократ» или «Plato» используются в пространствах.

Обозначение абзацев

Основной лингвистический элемент - это «линия идентичности», толстая линия любой формы. Строка идентичности стыкуется с пустым пространством предиката, чтобы показать, что предикат применяется по крайней мере к одному человеку. Чтобы выразить, что предикат «_ is a person» применяется по крайней мере к одному человеку - чтобы сказать, что существует (по крайней мере) один человек, - нужно записать строку идентичности в пространстве предиката «_ is a person:»

Есть хоть один человек.
Логика предикатов: ∃xMensch (x)

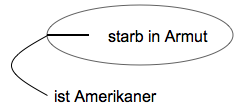
Если линия идентичности соединяет два или более пробелов - независимо от того, являются ли они разными предикатами или одним и тем же предикатом - тогда она выражает, что есть по крайней мере один человек, который - записанный в соответствующем пространстве - делает каждый из этих предикатов истинным одновременно. Простой пример - следующий абзац. На этом графике линия идентичности выражает, что существует по крайней мере один объект, который удовлетворяет как предикату «_ является американцем», так и предикату «_ умер в бедности» - другими словами, что есть по крайней мере один американец, который живет в Бедность умерла.

По крайней мере, один американец умер в бедности.
Логика предикатов: ∃x (Американцы (x) ∧ Смерть в бедности (x))

Следующее следует четко отличать от этого параграфа, который составлен в соответствии с правилами алфавитов:

Есть хоть один американец. По крайней мере, один человек умер в бедности.
Логика предикатов: ∃xAmericans (x) ∧ ∃yDying-in-Poverty (y)

В этом случае два отдельных абзаца пишутся один под другим. Верхний подграф указывает, что по крайней мере один человек выполняет предикат «_ американец», т.е. то есть есть американцы. Нижний подграф утверждает аналогичным образом, что по крайней мере один человек выполняет предикат «_ умер в бедности», т.е. то есть, по крайней мере, один человек умер в бедности. Написание двух абзацев рядом или один под другим означает, в соответствии с правилами алфавита, утверждать истинность обоих. Комбинированный график говорит о том, что есть по крайней мере один американец и что по крайней мере один человек умер в бедности, но он не утверждает, что люди, у которых есть один предикат, также имеют другой.

Посредством подходящей комбинации линии тождества с известными пропозициональными средствами альфографов можно сформулировать почти все утверждения логики предикатов.

Простой случай - отрицание утверждения о существовании. В следующем примере утверждение первого примера, т.е. То есть утверждение, что есть люди, опровергается тем, что написано в сокращении. Итак, утверждается, что это не тот случай, когда есть люди - на более красивом немецком языке: что нет людей.

Нет человеческой
логики предикатов: ¬∃xHuman (x)

Следующий график отличается от этого графика, на котором идентичная линия кажется выступающей из разреза:

Есть по крайней мере один человек, который не является человеком.
Логика предикатов: ∃x¬Human (x)

Согласно прочтению абзацев, существует связь между двумя графами: внешняя пустая линия идентичности, которая просто говорит: «Что-то существует»; и линия идентичности внутри разреза, которая говорит сама за себя: это не тот случай, когда есть хотя бы один Индивид, который выполняет предикат «_ есть человек». Соединение двух линий в точке, где они разрезают разрез, выражает идентичность репрезентативных индивидов: «Есть что-то, и это что-то не человеческое». Вышеупомянутый абзац не выражает ничего, кроме утверждения, что есть вещи не человек.

Линия идентичности, расположенная внутри разреза, может быть так же легко связана с внешней линией идентичности, которая, в свою очередь, стыкуется с предикатом. График ниже является примером этого созвездия. Сама по себе вырезка гласит: «Дело не в том, что кто-то умер в бедности; и само по себе внешнее выражение утверждает, что есть по крайней мере один человек, который является американцем. Поскольку оба выражения линий идентичности касаются друг друга на разрезе, общее выражение выражает идентичность обоих индивидов, поэтому оно говорит: есть по крайней мере один американец, который не умер в бедности.

Есть по крайней мере один американец, который не умер в бедности
Логика предиката: ∃x (американцы (x) ∧¬Dying in бедность (x))

Общее утверждение типа «Все свиньи розовые» будет представлено абзацем следующего типа. Буквально это отрицание предложения типа из предыдущего примера, в частности отрицание «есть по крайней мере одна свинья не розового цвета». Однако отрицать, что есть не розовые свиньи, теперь означает сказать что все свиньи на самом деле розовые.

Все свиньи розовые.
Логика предикатов: ∀x (Свинья (x) → Розовый (x)) или буквально ¬∃x (Свинья (x) ∧¬Rosa (x))

Если линия идентификации помечена пустым разрезом, как в следующем примере, это выражает неидентификационные данные лиц, которые заполняют места, к которым стыкуется линия идентификации. В этом смысле пример напротив говорит о том, что есть по крайней мере одна свинья и что есть по крайней мере одна розовая особь, но оба они не идентичны.

Есть хоть одна свинья и есть хоть одна розовая вещь, которая не то же самое.
Логика предикатов: ∃x∃y (Pig (x) ∧Pink (y) ∧¬x = y)

По аналогии с предыдущим параграфом, в следующем параграфе говорится, что есть по крайней мере две свиньи: «Есть свинья, и есть (другая) свинья, которая не идентична предыдущей».

Есть как минимум две свиньи.
Логика предикатов: ∃x∃y (Pig (x) ∧Pig (y) ∧¬x = y)

Заключительные правила абзацев

В системе абзацев не добавляются настоящие правила вывода логики предикатов, но изменяются существующие правила. Подробно знакомые окончательные правила имеют следующую новую формулировку:

R1 - Правило стирания

Любой оператор, который находится на уровне с четным номером, и любая часть строки идентификатора, которая встречается на уровне с четным номером, может быть удалена без замены.

Применение правила удаления (R1)

R2 - Правило вставки

Любой оператор может быть вставлен на уровне с нечетным номером, и два или более несвязанных конца идентификационных линий могут быть соединены друг с другом по желанию.

Применение правила вставки (R2)

R3 - Правило итерации

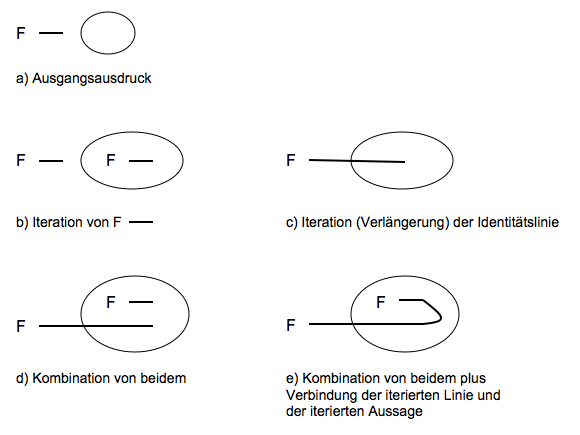
Любой оператор, который является частью составного оператора, может повторяться на том же уровне или ниже, но не внутри себя. Для строк идентичности разрешены следующие итерации:

1. Дополнительная идентификационная линия с незакрепленным концом может быть добавлена ​​к существующей идентификационной линии в любое время, т.е. ЧАС. линия идентичности, которая не стыкуется ни с одним пространством в предикате или с любой другой строкой идентичности. Приведенная таким образом линия идентичности не должна касаться разреза или пересекать его.
2. Каждая линия идентичности с незакрепленным концом может быть расширена так, чтобы ее новый конец оказался на том же или более низком уровне.
3. Итерация оператора и итерация строки идентификатора могут быть объединены друг с другом таким образом, что свободный конец повторяющейся строки идентификатора соединяется с повторяющимся оператором.

Применение правила повторения (R3)

R4 - Отмена повторения («Правило деитерации»)

Если утверждение X формально имеет форму, которая могла бы возникнуть из утверждения Y, применяя R3, правило повторения, то R4 может использоваться для вывода от X к Y; не обязательно, что X действительно возник в результате применения R3.

R5 - Правило двойного удара

Двойные разрезы могут быть вставлены и удалены по желанию как вокруг существующих операторов, так и сами по себе. Повторяющиеся вырезы также могут быть вставлены таким образом, чтобы они пересекали линии идентичности, но оба вставленных выреза всегда должны пересекать все линии разрезов.

Дальнейшие примеры

набухать

1. ^ «Развитие логики первого порядка независимо от Фреге, предвосхищение нормальных форм пренекса и Сколема» (Hammer 1998, стр. 489)
2. ↑ «Пирс хочет знак, который не просто будет пониматься общепринятым [...], но который будет« носить свое значение на рукаве », так сказать» (Zeman 1964, стр. 21, цитата из онлайн-издания)
3. ↑ «[алгебраические формулы] не являются« иконическими »- то есть они не похожи на объекты или отношения, которые они представляют. Пирс счел это дефектом »(Робертс, 1973, стр. 17).
4. ↑ «Графических публикаций [Пирса] было немного, и их было непросто понять, как он сам признал» (Робертс 1973, стр. 12)
5. ^ «[T] синтаксис графов Пирса не обладает, по крайней мере, в целом, комбинаторной элегантностью и простотой линейных обозначений» (Hammer 1998, стр. 502)
6. ↑ Робертс указывает, что даже стандартная работа по истории логики, Книл / Книл : Развитие логики. Кларендон Пресс. Oxford 1962, ISBN 0-19-824773-7 , не говоря уже о логических диаграммах Пирса.
7. ↑ «Можно сомневаться в эффективности диаграмм Пирса […]. Их основной механизм слишком сложен […] ». (Куайн: Обзор сборников статей Чарльза Сандерса Пирса, том 4: Простейшая математика, Исида 22, стр. 552, цитата из Робертса 1973, стр. 13)
8. ^ "Помимо их исторического интереса, графические формализмы Пирса представляют актуальный интерес. Система концептуальных графов Совы […] основана на работе Пирса. [Другая работа] также указывает на растущий интерес к логике графических рассуждений »(Hammer 1998, стр. 489).
9. ↑ см., Например, Б. Сун Чжу Шин: «Восстановление бета-графов в эффективную систему», Архив журнала логики, языка и информации, том 8, выпуск 3, июль 1999 г., страницы 273–295
10. ↑ Доказательства этого были представлены Дж. Джеем Земаном в его диссертации в 1964 г. (см. Список литературы); для альфографов см. также работу Уайта, 1984
11. ↑ Точнее, но не так понятно: с тем фактом, что «основной символ» параграфов выражает «отношение существования» (цитата из Робертса, стр. 30)
12. ↑ Письмо Уильяму Джеймсу, 18 декабря 1897 г., цитата из Робертса, стр.30.
13. ↑ Изложение правил вывода и их нумерация следует из презентации в книге Дона Д. Робертса «Экзистенциальные графы Чарльза С. Пирса» , стр. 40-45.
14. ↑ В презентации особенно внимательно следует Робертс, стр. 56–60.

литература

Первичная литература

• Чарльз Хартшорн , Пол Вайс (ред.): The Collected Papers of CS Peirce , Cambridge: Harvard 1931-35 (перепечатка тома 3 и тома 4: Harvard University Press 1987, ISBN 0-674-13801-5 ) - в частности, страницы 320 -470 и 530-572 Тома IV. Доступно в Интернете:
  • «Символьная логика» и «Экзистенциальные графы» (CP 4.372–417)
  • «Об экзистенциальных графах, диаграммах Эйлера и логической алгебре» и «Гамма-часть экзистенциальных графов» (CP 4.418–529)
  • «Пролегомены к апологии прагматизма» (CP 4.530–572)
  • «Улучшение гамма-графиков» (CP 4.473-584)

Вторичная литература

Монографии

• Дон Д. Робертс: Экзистенциальные графы Чарльза С. Пирса , Гаага: Мутон 1973 (= подходы к семиотике 27) - стандартная вводная работа к экзистенциальным графам на английском языке.
• Sun-Joo Shin: The Iconic Logic of Peirce's Graphs, Кембридж, Массачусетс: MIT Press, Bradford 2002, ISBN 0-262-19470-8 - последняя монография по этому вопросу
• Дж. Джей Земан: Графическая логика Ч. С. Пирса , Чикаго: 1964 (диссертация), доступна в Интернете по адресу [1] - новаторская, очень формальная презентация, в которой, среди прочего, показана полнота и правильность альфа- и бета-абзацев

Предметы

• Эрик М. Хаммер: Семантика экзистенциальных графов, Журнал философской логики , том 27, выпуск 5 (октябрь 1998 г.), страницы 489-503
• Деннис Хиггинс, Брэм Ван Хьювельн, Элизабет Хэтфилд, Дебора Килпатрик, Лут Вонг: «Реализация Java для экзистенциальных графов Пирса», Журнал компьютерных наук в колледжах , том 16, выпуск 3, март 2001 г., онлайн за плату под  [2] - рассматривается реализация Java, но представляет собой краткое введение в альфаграфы
• Ричард Б. Уайт, "Альфа-графы Пирса: полнота логики высказываний и быстрое упрощение функций истины", Труды Общества Чарльза С. Пирса , том 20, номер 4, 1984, стр. 351-361

веб ссылки

• Эрик Хаммер:  дедуктивная логика Пирса. В: Эдвард Н. Залта (Ред.): Стэнфордская энциклопедия философии .
• Мэри Киллер: философский контекст экзистенциальных графов Пирса
• Экзистенциальные графы MS 514 Чарльза Сандерса Пирса с комментариями Джона Ф. Сова (английский)
• Peirce Edition Project (английский)
• Peirce Proof Builder - Java-апплет для интерактивной проверки в системе алфавитов Пирса
• Домашняя страница Dr. Фритджоф Дау с обширным материалом по теме экзистенциальных графов (включая сканирование оригинальных заметок Пирса о экзистенциальных графах MS 145)

Эта статья была добавлена в список отличных статей 1 декабря 2006 года в этой версии .