Метод конечных элементов

Визуализация FEM-моделирования деформации автомобиля при асимметричном лобовом столкновении

Представление распределения тепла в корпусе насоса с помощью уравнения теплопроводности . «Конечные элементы» можно увидеть с краями элементов в виде черных линий.

Метод конечных элементов (МКЭ), также известный как « метод конечных элементов », представляет собой общий численный метод, используемый для различных физических задач . Наиболее известным является применение метода конечных элементов в прочности и деформации анализа из твердых тел с геометрически сложных форм, так как здесь применение классических методов (например , в теории пучка ) оказывается слишком много времени или не представляется возможным. Логически МКЭ основан на численном решении сложной системы дифференциальных уравнений .

Расчетная область (например, как твердые тела) проще в конечном числе подобластей (z. B. частичное тело), разделенных таковой. Б. во многих малых кубоидах или тетраэдрах . Это «конечные элементы». Благодаря их простой геометрии их физическое поведение можно хорошо рассчитать с помощью известных функций формы . Физическое поведение всего тела моделируется тем, как эти элементы реагируют на силы, нагрузки и граничные условия, и как нагрузки и реакции распространяются при переходе от одного элемента к другому из-за очень специфических проблемно-зависимых условий непрерывности, к которым приближается функции должны выполнять.

Функции подхода содержат параметры, которые обычно имеют физический смысл, такие как Б. смещение определенной точки компонента в определенный момент времени. Таким образом, поиск функции движения сводится к поиску значений параметров функций. Точность приближенного решения можно повысить, используя все больше и больше параметров (например, все больше и больше, меньшие элементы) или все более и более ценные функции подхода.

Разработка FEM была возможна только на существенных этапах с помощью разработки мощных компьютеров, так как для этого требуются значительные вычислительные мощности. Таким образом, этот метод с самого начала был сформулирован в удобной для компьютера манере. Это привело к значительному прогрессу в обработке вычислительных областей любой формы.

вступление

Сгенерированная структурная модель поршневого поршня (дизельного двигателя) как компонента двигателя внутреннего сгорания с целью анализа напряжений

С помощью FEM можно рассчитывать задачи из различных физических дисциплин, поскольку это, по сути, численный метод решения дифференциальных уравнений . Во-первых, расчетная область («составляющая») разбивается на большое количество элементов - достаточно мелких. Эти элементы конечно малы, но их фактический размер остается математически значимым - они не «бесконечно малы» (бесконечны). Разделение области / компонента на определенное количество элементов конечного размера, которые можно описать конечным числом параметров, дало методу название «метод конечных элементов».

Для этих элементов существуют функции формы (например, локальные подходы Ритца для каждого элемента), которые описывают, как элемент реагирует на внешние воздействия и граничные условия. Если вы вставите эти функции формы для всех элементов в решаемые дифференциальные уравнения, которые описывают физические законы, вы получите в основном очень большую систему уравнений вместе с начальными, граничными и переходными условиями. Решить ее (хотя бы приблизительно) - задача решателя уравнений КЭ. Размер решаемой системы уравнений во многом зависит от количества конечных элементов. Его приближенное решение в конечном итоге представляет собой численное решение рассматриваемого дифференциального уравнения; Если для всех элементов решено, как они ведут себя под нагрузками, то это также приводит к реакции всего компонента.

Конечное, бесконечное

Математически размер каждого элемента остается актуальным и также должен учитываться при его вычислении, он просто «конечно» мал. В случае «бесконечно» малых элементов их размер будет незначительным и больше не будет учитываться в уравнениях. В связи с этим остается актуальным размер элемента.

«Достаточно тонкое» разделение компонента на элементы присутствует, если дальнейшее уточнение больше не оказывает существенного влияния на результат расчета. И. Э. общий результат не зависит от размера элемента, который (с этой точки зрения) больше не актуален. Если размер элемента по-прежнему оказывает значительное влияние на общий результат, применяется i. A. сетка недостаточно тонкая.

история

Практическое использование МКЭ началось в 1950-х годах с расчета конструкции крыльев самолетов в аэрокосмической промышленности ( Turner , Clough, 1956), а вскоре и в автомобилестроении. Этот метод основан на работе Daimler AG в Штутгарте, в которой использовалась разработанная пользователем программа FEM ESEM (Elastostatic Element Method) задолго до того, как в начале 1980-х годов было внедрено компьютерное проектирование (CAD). Термин "метод конечных элементов" был впервые предложен Р. В. Клафом в 1960 году и используется повсеместно с 1970-х годов. Самый распространенный немецкоязычный термин для промышленных пользователей - это инженер-счетчик .

История метода конечных элементов вытекает из исследований и публикаций следующих авторов (выборка):

• Карл Генрих Шельбах : Вариационное исчисление ; Решение задачи минимальной площади (1851/52)
• Эрнст Густав Кирш: Основные уравнения теории упругости твердых тел, выведенные из рассмотрения системы точек, соединенных упругими подпорками (1868 г.)
• Джон Уильям Стратт, третий барон Рэлей (1842-1919): К теории резонанса. 1870 г.
• Вальтер Ритц (1878–1909): новый метод решения вариационных задач, метод Ритца (1908/09)
• Борис Г. Галеркин (1871–1945): Метод взвешенных остатков (1915)
• Эрих Треффц (1926): локально ограниченные функции подхода; Аналог метода Ритца
• Ганс Эбнер (1929): Шубблех как элемент уровня в авиастроении
• Александр Хренникофф (1896–1984): стержневые модели, замена окон на каркас, панели с опорными решетками 1940/41
• Ричард Курант (1888–1972): вариационные методы решения проблем равновесия и вибрации. 1943 г. (функции подхода с местной опорой, поэлементные подходы к проблемам вибрации)
• Уильям Прагер (1903–1980), Джон Лайтон Синг (1897–1995): приближение в области упругости на основе концепции функционального пространства. 1947 г.
• Джон Аргирис (1913-2004): метод силы и смещения для стержневых конструкций, матричная формулировка (1954/55)
• MJ Turner, Ray W. Clough , HC Martin, LJ Topp: Анализ жесткости и прогиба сложных конструкций. 1956 (первый структурный расчет крыльев самолета в компании Boeing , первое применение МКЭ с компьютерной программой, первое применение элементов поверхности)
• Рэй В. Клаф (1920-2016): Метод конечных элементов в анализе плоских напряжений. 1960 (вероятно, первое использование термина конечные элементы)
• Spierig (1963): Разработка треугольных элементов, переход на раковины
• Ольгерд Сесил Зиенкевич (1921–2009), пионер МКЭ и первая стандартная работа (учебник): Метод конечных элементов в структурной механике и механике сплошной среды , 1967 (совместно с Ю.К. Чунгом)
• Альфред Циммер (* 1920) и Петер Грот (* 1938), пионеры МКЭ, первый немецкий учебник МКЭ: Элементный метод эластостатики , 1969 г. Oldenbourg Verlag, Мюнхен, Вена
• Ольга Александровна Ладищенская (1922–2004), Иво Бабушка (* 1926) и Франко Брецци (* 1945) - условие Ладищенской-Бабушки-Брецци устойчивости смешанной задачи конечных элементов со структурой седловой точки
• Иво Бабушка (* 1926) - адаптивные алгоритмы конечных элементов

заявление

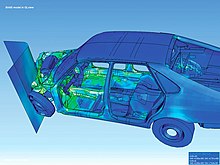
Первым применением МКЭ была линейная обработка твердых тел и структур в форме метода смещения, и на его основе МКЭ получал свои импульсы. Термин «конечные элементы» был использован несколько позже. В ходе дальнейших исследований метод конечных элементов все более обобщался и теперь может быть использован во многих физических задачах, в том числе может использоваться в различных полевых расчетах, прогнозах погоды или для решения технических проблем в автомобильной, медицинской, аэрокосмической, машиностроительной отраслях промышленности или производстве товаров народного потребления. Одной из основных областей применения метода является разработка продукции , при которой, среди прочего, рассчитываются расчеты механической прочности отдельных компонентов или, например, конструкции шасси и кузова в целом, чтобы сэкономить время, необходимое для краш-тестов .

Процедура линейного механического расчета (примерная)

Программы, использующие метод конечных элементов, работают по принципу EVA : пользователь создает (компонентную) геометрию в программе САПР. Затем он делает дальнейшие записи в так называемом препроцессоре FE . Решатель уравнений FEM выполняет фактические вычисления, и пользователь получает результаты вычислений, которые он затем может просматривать в так называемом постпроцессоре FE в форме графических дисплеев. Часто препроцессор и постпроцессор объединены в одной программе или даже являются частью программы САПР.

Расчет линейной прочности технологической цепи

Вход: препроцессор

Компонент предназначен в CAD программы и переданы в препроцессор FE , используя прямой интерфейс или нейтральный обменный формат , такой как STEP . Путем выбора сетевых параметров, таких как размер элемента и тип элемента (например, тетраэдр, шестигранник в 3D) в модуле создания сетки, конечные элементы генерируются с помощью алгоритма создания сетки. Для анализа механической прочности необходимо ввести поведение материала, которое по существу указывает, какие реакции компонент имеет на внешние нагрузки (например, деформацию). В зависимости от материала соотношение между напряжением и деформацией разное, и бывают разные деформации. Если это соотношение является линейным, для расчета КЭ требуются только модуль упругости и коэффициент Пуассона , в противном случае требуются дополнительные параметры материала и входные данные в препроцессор. Другими граничными условиями являются, например, нагрузки, действующие на компонент (силы, давление, температура и т. Д.). Чтобы получить максимально реалистичное представление, задаются однородные (ограничения) и неоднородные граничные условия (смещения), а также все нагрузки, которые необходимо учитывать в модели.

Обработка: решатель уравнений

В зависимости от программы используется отдельная (автономная программа) или интегрированная программа решения уравнений. Он рассчитывает моделирование того, как нагрузки, силы и граничные условия влияют на отдельные элементы компонента, и как силы и эффекты распространяются в компоненте и влияют на соседние элементы. Расчет сначала дает грубое приближенное решение. Дальнейшие итерации улучшают приближение. Большинство итераций рассчитываются до тех пор, пока не будут внесены только самые незначительные изменения - тогда приближение «сойдется» и является результатом моделирования.

Выход: постпроцессор

В случае расчета механической прочности пользователь получает результат решателя уравнения МКЭ в конкретных значениях напряжения , деформации и удлинения . Постпроцессор может отображать это, например, в изображении в ложных цветах . Эти эквивалентные значения напряжения используются, например, для проверки на прочность компонента.

Общая функциональность

Дискретность

Метод конечных элементов - это дискретный метод; ЧАС. решение вычисляется на дискретном подмножестве базовой области. Для этого он разбит на простые подобласти, так называемые конечные элементы (сети, сетка). Термин «конечный» подчеркивает отличие от аналитического рассмотрения бесконечно малых элементов. Углы конечных элементов называются узлами. Эти узлы образуют дискретное подмножество для численного метода. Функции аппроксимации вводятся на элементах, которые содержат в качестве параметров неизвестные размеры узлов. Локальные приближения вводятся в слабую постановку краевой задачи. Результирующие интегралы элементов вычисляются с помощью числовой квадратуры. Подходы аппроксимации «интегрированы», так что только значения узлов остаются на элементах как неизвестные после интегрирования. Уравнения элементов составляются с учетом требований непрерывности на границах элементов. Таким образом, краевые задачи для линейных дифференциальных уравнений в частных производных преобразуются в линейную систему уравнений с симметричными матрицами системы. Для нелинейных дифференциальных уравнений алгоритм работает аналогично с той разницей, что нелинейные зависимости итеративно линеаризуются подходящими методами (например, методом Ньютона), а линейная система уравнений настраивается для возрастающих величин на каждом подэтапе.

Пример использования адаптивной сетки для расчета воздушного потока вокруг крыла самолета.

Для определенных задач разделение на элементы в значительной степени предопределено проблемой, например, в случае пространственных каркасов, в которых отдельные стержни образуют элементы конструкции. Это также относится к каркасным конструкциям, где отдельные балки или отдельные части балки представляют собой элементы задачи. В случае двумерных задач основная область делится на треугольники или квадраты. Даже если используются только прямые элементы, очень хорошее приближение к основной площади может быть достигнуто с соответствующей тонкой дискретизацией . Криволинейные элементы повышают качество аппроксимации. В любом случае эта дискретизация позволяет гибко записывать базовую область, которая также адаптирована к проблеме. Однако следует соблюдать осторожность, чтобы избежать очень острых или тупых углов в угловых узлах элемента, чтобы исключить численные трудности. Затем данная область заменяется областью аппроксимирующих элементов. Тест патча позже может быть использован для проверки , работает ли это хорошо.

Пространственные задачи решаются с разделением трехмерной области на тетраэдрические элементы , кубовидные элементы или другие элементы, адаптированные к задаче, возможно, также с изогнутыми краями, это i. d. Р. Серендипити или элементы Лагранжа , под ред.

Тонкость подразделения, т.е. ЧАС. плотность сети имеет решающее влияние на точность результатов приближенного расчета. Поскольку вычислительные усилия возрастают при использовании более тонких и плотных сетей, важно разрабатывать сетевые решения, которые являются как можно более интеллектуальными .

Элементный подход

В каждом из элементов выбирается проблемно-ориентированный подход к искомой функции или, в более общем смысле, к функциям, которые описывают проблему. Для этого особенно подходят целые рациональные функции в независимых пространственных координатах. Для одномерных элементов (стержней, балок) рассматриваются полиномы первой, второй, третьей, а иногда и более высокой степени. В случае двумерных задач используются линейные, квадратичные полиномы или полиномы более высокого порядка. Тип подхода зависит, с одной стороны, от формы элемента, а с другой стороны, решаемая проблема также может влиять на выбор подхода. Потому что функции подхода должны удовлетворять очень специфическим проблемно-зависимым условиям непрерывности при переходе от одного элемента к другому . Требования непрерывности часто очевидны по физическим причинам, а также необходимы по математическим причинам. Например, перемещение связного тела в одном направлении должно быть непрерывным при переходе от одного элемента к другому, чтобы гарантировать непрерывность материала. В случае изгиба балки или пластины требования к непрерывности выше, потому что там по аналогичным физическим причинам должна требоваться непрерывность первой производной или первых двух частных производных. Элементы с функциями формы, удовлетворяющими условиям непрерывности, называются конформными.

Чтобы действительно удовлетворить требованиям непрерывности, кривая функции в элементе должна быть выражена значениями функции, а также значениями (частных) производных (смещения узловых точек) в определенных точках элемента, узловых точках . Значения функций и значения производных, используемых в узлах, называются узловыми переменными элемента. С помощью этих узловых переменных функция приближения представлена ​​как линейная комбинация так называемых функций формы с узловыми переменными в качестве коэффициентов.

Рекомендуется использовать глобальную систему координат для координат узла в дополнение к локальной системе координат, связанной с элементами. Оба связаны функциями преобразования. Если для этого преобразования используются те же функции формы, что и для метода деформации, то они являются изопараметрическими элементами для функций субпараметрических или суперпараметрических элементов более низкой или более высокой степени.

граничные условия

После дискретизации данной задачи и настройки матриц элементов вводятся заданные граничные условия . Типичная проблема FE может иметь два типа граничных условий: условия Дирихля и граничные условия Неймана . Они всегда применяются (работают) в узлах.

Граничное условие Дирихле напрямую определяет значение функции, а граничное условие Неймана определяет производную от значения функции. Если задано граничное условие Дирихле, это означает, что задача получает на одну степень свободы меньше, а соответствующие строка и столбец в общей матрице удаляются. Если граничное условие Дирихле не равно нулю, значение добавляется к линейной форме («правая часть») в соответствии с его предварительным коэффициентом. В зависимости от типа физической проблемы могут быть задействованы различные физические величины, как показано в качестве примера в таблице. Граничные условия Неймана также имеют долю в линейной форме («правая часть»).

Еще одним вариантом являются периодические граничные условия , в которых значения на одном крае берутся в качестве данных для другого края и, таким образом, моделируется периодически бесконечно продолжающаяся область. Для вращательно-симметричных задач определены так называемые циклические граничные условия.

Основные уравнения метода перемещений

Метод смещения - это стандартная формулировка метода конечных элементов, в котором смещения являются первичными неизвестными, описывающими перемещение, вращение и деформацию твердого тела. Метод смещения доступен во всех распространенных программах конечных элементов, с помощью которых могут быть рассчитаны задачи механики твердого тела. Есть несколько основных уравнений для решения задач твердого тела .

Принцип Даламбера в лагранжевой версии

Одним из уравнений, лежащих в основе метода смещения, с помощью которого могут быть решены общие проблемы механики твердого тела, является принцип Даламбера , сформулированный в лагранжевом описании механики сплошных сред . С помощью этого принципа можно анализировать как линейные проблемы, такие как вопрос о собственных колебаниях, так и крайне нелинейные проблемы, такие как краш-тесты . Здесь используется метод взвешенных остатков по Галеркину, также называемый методом Галеркина или подходом Галеркина.

Принцип минимума потенциальной энергии

В консервативных системах , в случае статической задачи, узловые смещения могут быть определены из условия, что потенциальная энергия имеет минимум в желаемом состоянии равновесия . С помощью принципа минимума потенциальной энергии уравнения жесткости конечных элементов могут быть определены напрямую. Потенциальная энергия конструкции - это сумма внутренней энергии деформации (энергии упругой деформации) и потенциала приложенных нагрузок (работа, совершаемая внешними силами).

Метод длины дуги

Метод длины дуги - это метод, с помощью которого можно вычислить с управлением по усилию до максимальной допустимой нагрузки. Необходимость методов, управляемых силой, заключается в том, что, в отличие от методов, управляемых смещением, можно прямо пропорционально увеличивать многократные нагрузки. При использовании метода длины дуги нагрузка увеличивается, как указано; Если это увеличение нагрузки приведет к слишком большой деформации, нагрузка умножается на коэффициент меньше 1 и даже с отрицательными значениями после достижения допустимой нагрузки.

Стохастический метод конечных элементов

В варианте стохастического метода конечных элементов (SFEM) входные переменные модели, которые подвержены неопределенности, например прочность материала или нагрузки, моделируются с использованием стохастических переменных. Этого можно добиться с помощью обычных случайных величин . Также часто используются случайные поля , которые представляют собой случайно изменяющиеся непрерывные математические функции. Распространенным методом расчета является моделирование Монте-Карло . Расчет FE повторяется для многих случайных реализаций ( выборок ) входных переменных до тех пор, пока одна из них не упадет ниже определенной заранее определенной стохастической ошибки. Моменты, то есть среднее значение и дисперсия, затем вычисляются по всем результатам. В зависимости от разброса входных переменных часто требуется много повторений расчета FE, что может занять много вычислительного времени.

Неявные и явные решатели FE

Конструктивно-механические системы МКЭ представлены линейными системами уравнений 2-го порядка:

${\ Displaystyle M {\ ddot {u}} (t) + D {\ dot {u}} (t) + Ku (t) = P (t)}$

${\ displaystyle M, D}$и - матрица массы, демпфирования и жесткости системы; - вектор внешних сил, действующих на модель. - вектор степеней свободы. ${\ displaystyle K}$${\ Displaystyle P (t)}$${\ displaystyle u}$

Сложные модели компонентов часто состоят из нескольких миллионов узлов, и каждый узел может иметь до 6 степеней свободы. Поэтому решатели FEM (решатели системы уравнений) должны отвечать определенным требованиям в отношении эффективного управления памятью и, при необходимости, использования нескольких процессоров. Существует два принципиально разных типа решателей МКЭ: неявные и явные.

Неявные решатели FEM делают определенные предположения, при которых рассчитанный вектор решения является действительным. Акты з. Б. временно неизменная нагрузка на систему с демпфированием, то по прошествии достаточно длительного времени установится постоянный вектор смещения . Тогда для есть , и система уравнений упрощается до с решением${\ displaystyle u}$${\ Displaystyle P (t) = P = const.}$${\ displaystyle u (t) = u = const.}$${\ Displaystyle т \ к \ infty}$${\ displaystyle {\ ddot {u}} (t) = {\ dot {u}} (t) = 0}$${\ displaystyle Ku = P}$${\ displaystyle u = K ^ {- 1} P}$

Для данного вектора нагрузки вектор смещения может быть вычислен с использованием алгоритма Гаусса или QR-разложения . ${\ displaystyle P}$${\ displaystyle u}$${\ displaystyle K}$

Если механическая система подвергается гармоническому возбуждению , может потребоваться определение собственных частот системы, чтобы избежать резонансов во время работы. ${\ Displaystyle P (T) = {\ Hat {P}} \ sin (\ Omega t)}$

Собственные частоты - это все частоты, для которых вектор смещения представляет собой решение системы уравнений без нагрузки ( ) и незатухания ( ). Следующее далее применимо к вектору скорости и ускорения. ${\ displaystyle \ omega _ {я}}$${\ Displaystyle и (т) = {\ шляпа {и}} _ {я} \ грех (\ омега _ {я} т)}$${\ Displaystyle P (t) = 0}$${\ displaystyle D = 0}$

${\ displaystyle {\ dot {u}} _ {i} = {\ hat {u}} _ {i} \ \ omega _ {i} \ cos (\ omega _ {i} t), \ {\ ddot { u}} _ {i} = - {\ hat {u}} _ {i} \ omega _ {i} ^ {2} \ sin (\ omega _ {i} t)}$

и система уравнений, таким образом,

${\ displaystyle (-M \ omega _ {i} ^ {2} + K) {\ hat {u}} _ {i} \ sin (\ omega _ {i} t) = 0}$

Чтобы вычислить собственные частоты и связанные с ними собственные моды , неявный решатель должен решить проблему собственных значений ${\ displaystyle \ omega _ {я}}$${\ displaystyle {\ hat {u}} _ {i}}$

${\ displaystyle -M \ omega _ {i} ^ {2} + K = 0}$

решать.

Явные решатели МКЭ

Явные решатели вычисляют векторы смещения в определенные дискретные моменты времени в пределах заданного интервала времени. Скорости и ускорения узлов аппроксимируются коэффициентами разницы смещений в последовательные моменты времени . При постоянном шаге по времени применяется следующее: ${\ displaystyle u_ {i}}$${\ displaystyle t_ {i}}$${\ Displaystyle и_ {я + 1}, и_ {я}, и_ {я-1}}$${\ Displaystyle т_ {я + 1}, т_ {я}, т_ {я-1}}$${\ displaystyle t_ {я + 1} -t_ {i} = \ Delta \ t}$

${\ displaystyle {\ dot {u}} = {\ frac {u_ {i} -u_ {i-1}} {\ Delta \ t}}}$

${\ displaystyle {\ ddot {u}} = {\ frac {{\ frac {u_ {i + 1} -u_ {i}} {\ Delta \ t}} - {\ frac {u_ {i} -u_ { i-1}} {\ Delta \ t}}} {\ Delta \ t}} = {\ frac {u_ {i + 1} -2u_ {i} + u_ {i-1}} {(\ Delta t) ^ {2}}}}$

дискретизированная система уравнений имеет вид

${\ displaystyle M {\ frac {u_ {i + 1} -2u_ {i} + u_ {i-1}} {(\ Delta t) ^ {2}}} + D {\ frac {u_ {i} - u_ {i-1}} {\ Delta \ t}} + Ku_ {i} = P_ {i}}$

Решая это уравнение, получается соотношение, с помощью которого можно определить вектор смещения из ранее вычисленных векторов и : ${\ displaystyle u_ {я + 1}}$${\ displaystyle u_ {i}}$${\ displaystyle u_ {i-1}}$

${\ displaystyle u_ {я + 1} = M ^ {- 1} ((\ Delta t) ^ {2} (P_ {i} -Ku_ {i}) - D \ Delta \ t (u_ {i} -u_ {i-1})) + 2u_ {i} -u_ {i-1}}$

Вычисление обратного не выполняется на практике, поскольку явные решатели обычно предполагают диагональную матрицу, и поэтому каждая строка системы уравнений должна быть разделена только диагональной записью в соответствующей строке . ${\ displaystyle M ^ {- 1}}$${\ displaystyle M}$${\ displaystyle M}$

Явные решатели используются, среди прочего, в конструкции транспортных средств для расчета случаев аварийной нагрузки.

Преимущество решателей прямых уравнений по методу Гаусса заключается в практическом применении в численной устойчивости и получении точного результата. Недостатками являются плохое кондиционирование обычно мало заполненных матриц жесткости и высокие требования к хранению, как упоминалось выше. Итерационные решатели менее чувствительны к плохому кондиционированию и требуют меньше памяти при использовании хранилища ненулевых элементов. Однако итеративные решатели используют критерий завершения для вычисления результатов. Если это будет достигнуто до того, как будет найдено приблизительно точное решение, результат, например кривая напряжения, может быть легко истолкован неверно.

В некоторых реализациях для часто встречающихся разреженных матриц сохраняются только позиции и значения записей, которые отклоняются от нуля. Это позволяет вам продолжать решать системы уравнений напрямую, но экономит много места в памяти.

Изогеометрический анализ

Некоторые программы могут адаптировать существующую сетку КЭ к (очень похожей, новой) геометрии САПР, которая обычно значительно меньше, чем в случае (незначительных) изменений в геометрии (САПР) компонента. Требуемое время.

Программ

Конечно-элементное программное обеспечение и его приложения - это сейчас многомиллиардная отрасль.

• На практике используется много разных больших автономных программ с аналогичным набором приложений; Выбор того, какую программу использовать, зависит не только от использования, но и от таких факторов, как доступность, стандарт сертификации в компании или стоимость лицензии.
• С помощью пакетов конечных элементов, интегрированных в коммерческие системы САПР , можно рассчитать более простые (обычно линейные) задачи, а затем непосредственно оценить их с помощью системы САПР. Отдельные шаги, например B. сетевой процесс (создание сетки ) выполняется автоматически в фоновом режиме.
• Поскольку для выполнения расчетов иногда требуется много вычислительной мощности, первые компании предоставляют вычислительные мощности своим пользователям в виде облачных сервисов.
• Существуют препроцессоры / постпроцессоры с графическим пользовательским интерфейсом и отдельные решатели FE.
• Существуют программные структуры без графического пользовательского интерфейса, в основном в виде препроцессора со встроенным решателем уравнений, которые управляются языком программирования, например, для управления решателем FE с помощью самодельных дополнительных подпрограмм.

Математический вывод

Рассматриваемая область решения сначала делится на подобласти , конечные элементы: ${\ displaystyle G}$${\ displaystyle G_ {1}, \ dotsc, G_ {m} \ subset G}$

${\ displaystyle G = \ bigcup _ {e = 1} ^ {m} G_ {e}}$.

Внутри находятся желаемая функция решения, теперь определены различные функции формы, которые представляют собой только несколько элементов, равных нулю, соответственно. Это свойство и есть настоящая причина появления термина «конечные элементы». ${\ displaystyle G}$${\ Displaystyle е \ двоеточие G \ в \ mathbb {R} ^ {k}}$${\ displaystyle \ psi _ {1}, \ dotsc, \ psi _ {n} \ двоеточие G \ to \ mathbb {R} ^ {k}}$

Возможные решения численной аппроксимации определяется с помощью линейной комбинации функций формы

${\ displaystyle f (x) = \ sum _ {i = 1} ^ {n} c_ {i} \ cdot \ psi _ {i} (x) \ quad, c_ {i} \ in \ mathbb {R}}$.

Поскольку каждая тестовая функция исчезает для большинства элементов, функция, ограниченная элементом, может, наоборот , быть описана линейной комбинацией меньшего числа тестовых функций . ${\ displaystyle G_ {e}}$${\ displaystyle f | G_ {e}}$${\ displaystyle \ psi _ {я}}$

Если дифференциальные уравнения и граничные условия задачи могут быть представлены в виде линейных операторов относительно функций , это приводит к линейной системе уравнений относительно свободных переменных линейной комбинации : ${\ displaystyle f}$${\ displaystyle c_ {i}}$

${\ Displaystyle D (c) = g}$

С участием

${\ displaystyle D}$= Линейное отображение в функциональное пространство${\ Displaystyle \ mathbb {R} ^ {п}}$

${\ displaystyle c}$ = Вектор коэффициентов линейной комбинации ${\ displaystyle c_ {i}}$

${\ displaystyle g}$ = Функция, представляющая дифференциальное уравнение и граничные условия

Чтобы получить конечную линейную систему уравнений, диапазон значений также моделируется с использованием функций приближения . Тогда это можно описать линейными комбинациями : ${\ displaystyle D}$${\ Displaystyle \ phi _ {1}, \ dotsc, \ phi _ {n}}$${\ displaystyle g}$${\ displaystyle \ phi _ {я}}$

${\ displaystyle g (x) = \ sum _ {i = 1} ^ {n} b_ {i} \ cdot \ phi _ {i} (x) \ quad, b_ {i} \ in \ mathbb {R}}$

и система уравнений получается в целом

${\ displaystyle A \ cdot c = b}$

С участием

${\ displaystyle A}$ = квадратная матрица с ${\ Displaystyle A = \ phi ^ {- 1} \ cdot D}$

${\ displaystyle c}$ = Вектор коэффициентов линейной комбинации ${\ displaystyle c_ {i}}$

${\ displaystyle b}$ = Вектор коэффициентов линейной комбинации ${\ displaystyle b_ {i}}$

Размер матрицы определяется числом функций приближения, умноженным на степени свободы, на которых основана физическая модель . Размерность матрицы - это количество полных степеней свободы, при этом спецификации, соответствующие модели в отношении уникальности задачи (например, смещения твердого тела в случае упругого тела), должны быть исключены. ${\ displaystyle k}$

Поскольку каждый элемент связан только с несколькими соседними элементами, большинство значений общей матрицы равны нулю, поэтому она «редко заполнена». В большинстве случаев используются одни и те же функции в качестве пакетных функций и функций тестирования . В этом случае матрица также симметрична относительно своей главной диагонали . ${\ displaystyle \ psi _ {я}}$${\ displaystyle \ phi _ {я}}$

Если число степеней свободы не слишком велико (примерно до 500 000), эта система уравнений может быть решена наиболее эффективно с использованием прямого метода , например, с помощью метода исключения Гаусса . Здесь можно эффективно использовать разреженную структуру системы уравнений. В то время как усилия по вычислению уравнений выполняются с помощью алгоритма Гаусса , усилия могут быть значительно сокращены за счет умного выбора точки поворота (например, алгоритма Марковица или теоретико-графических подходов ). ${\ displaystyle N}$${\ displaystyle {\ mathcal {O}} (N ^ {3})}$

Для более чем 500 000 неизвестных плохое состояние системы уравнений делает прямые решатели все более сложными, поэтому итерационные решатели, которые шаг за шагом улучшают решение, обычно используются для больших задач . Простыми примерами этого являются методы Якоби и Гаусса-Зейделя , но на практике используются многосеточные методы или методы предварительно обусловленных подпространств Крилова , такие как метод сопряженного градиента или метод GMRES . Из-за размера системы уравнений иногда необходимо использовать параллельные компьютеры.

Если уравнение в частных производных является нелинейным , результирующая система уравнений также будет нелинейной. Обычно это можно решить только с помощью методов численной аппроксимации. Примером такого метода является метод Ньютона , в котором линейная система решается шаг за шагом.

В настоящее время существует большое количество коммерческих компьютерных программ, использующих метод конечных элементов.

Слабая формулировка

Эллиптическое уравнение может быть сформулирована слабо, т.е.. ЧАС. проблема может быть выражена таким способом, который требует меньшей гладкости решения . Делается это следующим образом.

Для гильбертова пространства , функционала (функции из сопряженного с ним пространства) , а также для непрерывной и эллиптической билинейной формы решение вариационной задачи называется, если ${\ displaystyle H}$${\ displaystyle f \ in H ': = \ {g: \; H \ rightarrow \ mathbb {R} | \; g {\ text {линейный и непрерывный}} \}}$${\ displaystyle H}$ ${\ Displaystyle а (\ cdot, \ cdot)}$${\ displaystyle u \ in H}$

${\ Displaystyle а (и, v) = е (v) \ \ forall v \ in H}$.

Существование и единственность решения обеспечивает теорема представления Фреше Рисса (для случая, когда билинейная форма симметрична) или лемма Лакса-Милграма (общий случай). ${\ displaystyle u}$${\ displaystyle a}$

Мы знаем , что комната Гильберт номер . Исходя из этого, пространства Соболева можно определить с помощью так называемой слабой производной . ${\ Displaystyle L ^ {2} (\ Omega): = \ {е: \ Omega \ rightarrow \ mathbb {R} \ | \ \ | f \ | _ {L ^ {2}} <\ infty \}}$ ${\ Displaystyle H ^ {s} (\ Omega)}$

Задачу можно рассматривать как вариант дифференциального уравнения в частных производных в одной области . ${\ Displaystyle а (и, v) = е (v)}$${\ displaystyle \ Omega}$

Проблема Пуассона в качестве примера:

${\ Displaystyle - \ Delta и (х) = е (х) \ \ forall x \ in \ Omega}$

${\ Displaystyle и (х) = 0 \ \ forall х \ in \ partial \ Omega}$

где здесь обозначает в оператор Лапласа . Умножение с бесконечно часто непрерывно дифференцируемыми функциями получается после интегрирования ${\ displaystyle \ Delta}$${\ Displaystyle \ psi \ в C_ {0} ^ {\ infty} (\ Omega)}$

${\ displaystyle \ Leftrightarrow - \ int _ {\ Omega} \ Delta u \, \ psi \, dx = \ int _ {\ Omega} f \, \ psi \, dx \ \ forall \ psi \ in C_ {0} ^ {\ infty} (\ Omega).}$

Частичная интеграция (первая формула Грина ) и граничные условия для нулевой затем доставить ${\ displaystyle \ psi}$

${\ Displaystyle \ Leftrightarrow \ int _ {\ Omega} \ nabla u \, \ nabla \ psi \, dx = \ int _ {\ Omega} f \, \ psi \, dx \ \ forall \ psi \ in C_ {0 } ^ {\ infty} (\ Omega)}$

Теперь есть эллиптическая и непрерывная билинейная форма , а правая часть представляет собой непрерывную линейную форму.${\ Displaystyle а (и, \ psi): = \ int _ {\ Omega} \ nabla u \, \ nabla \ psi \, dx}$${\ Displaystyle H_ {0} ^ {1} (\ Omega): = {\ overline {C_ {0} ^ {\ infty} (\ Omega)}} ^ {\ | \ cdot \ | _ {H ^ {1 }}}}$${\ Displaystyle (е, \ фунт / кв. дюйм) _ {L ^ {2}} = е (\ фунт / кв. дюйм)}$${\ displaystyle H_ {0} ^ {1} (\ Omega)}$

Если рассматриваемое функциональное пространство / гильбертово пространство имеет конечный базис, линейная система уравнений может быть получена из вариационной формулировки.

Для функциональных помещений от выбора основы зависит эффективность процесса. Здесь часто используются сплайны с триангуляциями и, в некоторых случаях, дискретное преобразование Фурье (разбиение на синус и косинус).

Из соображений гибкости в отношении геометрии области обычно выбирается следующий подход. ${\ displaystyle \ Omega}$

Область дискретизируется путем деления ее на треугольники и использования сплайнов, связанных с вершинами p, для охвата конечномерного функционального пространства. Сплайны пересекаются в указанных точках треугольников (где δ - символ Кронекера ). Таким образом, вы можете представить дискретную функцию через ${\ displaystyle \ Omega}$${\ displaystyle \ lambda _ {p} (x)}$${\ displaystyle \ Omega}$${\ displaystyle \ lambda _ {p} (q) = \ delta _ {pq}}$${\ Displaystyle и_ {ч} (х)}$

${\ displaystyle u_ {h} (x) = \ sum _ {p} u_ {p} \, \ lambda _ {p} (x)}$

с коэффициентами, относящимися к базовому представлению. Из-за конечного базиса вам больше не нужно тестировать по всем базисным функциям, а только по всем базовым функциям; формулировка вариантов сокращается до из-за линейности ${\ displaystyle u_ {p}}$${\ displaystyle \ psi \ in H_ {0} ^ {1}}$

${\ displaystyle a (u_ {h}, \ lambda _ {q}) = \ sum _ {p} u_ {p} \, a (\ lambda _ {p}, \ lambda _ {q}) = (f, \ lambda _ {q}) \ \ forall q}$

Итак, мы получили систему линейных уравнений для решения

${\ Displaystyle А \ cdot и = е}$,

С участием

${\ displaystyle A_ {pq} = a (\ lambda _ {p}, \ lambda _ {q})}$

а также

${\ displaystyle f_ {q} = (f, \ lambda _ {q})}$

Этот результат получается для любого конечного базиса гильбертова пространства.

пример

Формальное определение конечного элемента (по Чиарле )

Конечный элемент - это тройка , где: ${\ Displaystyle Е = (Т, \ Пи, \ Сигма)}$

• ${\ displaystyle T}$ непустая область (например, треугольники, квадраты, тетраэдры и т. д.)
• ${\ displaystyle \ Pi}$- конечномерное пространство функций формы (линейных, квадратичных или кубических функций формы, то есть сплайнов; синусов и т. д.) функций формы${\ displaystyle \ rightarrow}$
• ${\ displaystyle \ Sigma}$представляет собой набор линейно независимых функционалов от узловых переменных${\ displaystyle \ Pi}$ ${\ displaystyle \ rightarrow}$

К функционалам относится то, что они связаны с функциями базы:

${\ displaystyle \ sigma _ {i} \ in \ Sigma: \ sigma _ {i} (\ pi _ {j}) = \ delta _ {ij} \ \ j \ in \ {1, \ ldots, \ dim ( \ Пи) \}}$

Так относится к каждой функции

${\ Displaystyle v \ in \ Pi: v (x) = \ sum _ {i} \ sigma _ {i} (x) \, \ pi _ {j}}$.

Для синуса как базисной функции im тогда ${\ Displaystyle \ mathbb {(} R) ^ {1}}$

${\ Displaystyle \ OperatorName {span} \, \ left \ {\ sin (x), \ sin (2x), \ ldots, \ sin (nx) \ right \} = \ Pi}$

и функционал

${\ displaystyle \ sigma _ {i} (\ psi): = (\ sin (ix), \ psi) _ {L ^ {2}}}$.

Для сплайнов, однако, оценка точки на указанных точках треугольников достаточно: . ${\ Displaystyle \ sigma _ {p} (\ psi): = \ psi (p)}$

S1: линейные элементы на треугольниках

Пространство МКЭ непрерывных кусочно-линейных функций определяется как:

${\ Displaystyle S ^ {1} (\ Omega, T): = \ left \ lbrace u \ in C ^ {0} (\ Omega) \; | \; {u |} _ {\ Delta} (x, y ) = a _ {\ Delta} + b _ {\ Delta} x + c _ {\ Delta} y \ quad \ forall \ Delta \ in T \ right \ rbrace}$,

где - область и триангуляция области с треугольниками и обозначает ограничение непрерывной функции на треугольник . ${\ displaystyle \ Omega \ subset \ mathbb {R} ^ {2}}$${\ displaystyle T \ subset \ Omega}$${\ displaystyle \ Delta}$${\ displaystyle {u |} _ {\ Delta}}$${\ displaystyle u}$${\ displaystyle \ Delta \ in T}$

P1: линейный опорный элемент на треугольнике

Ссылочный элемент определяется как: ${\ displaystyle {\ hat {T}}}$

${\ displaystyle {\ hat {T}} = \ left \ lbrace (x, y) \ in \ mathbb {R} ^ {2} | 0 <x <1 \; {\ text {and}} \; 0 < y <1-x \ right \ rbrace.}$

Эти линейные элементы являются функциями типа: ${\ displaystyle P1}$

${\ displaystyle p \ двоеточие {\ hat {T}} \ to \ mathbb {R}, (x, y) \ mapsto a + bx + cy \ quad {\ text {with}} \; a, b, c \ в \ mathbb {R}.}$

Для определения функции достаточно указать значения в угловых точках . Таким образом, все функции можно представить с помощью базовых функций : ${\ displaystyle p}$${\ displaystyle {\ has {E_ {1}}}: = (0,0), {\ has {E_ {2}}}: = (1,0), {\ has {E_ {3}}}: = (0,1)}$${\ displaystyle p}$${\ Displaystyle {\ шляпа {\ phi}} _ {я}}$

${\ displaystyle p (x, y) = \ sum _ {i = 1} ^ {3} \ alpha _ {i} {\ hat {\ phi}} _ {i} (x, y) \ quad {\ text {with}} \; \ alpha _ {i} \ in \ mathbb {R}.}$

Основные функции представлены в виде линейных функций, которые не равны нулю только в одной угловой точке:

${\ displaystyle {\ hat {\ phi}} _ {i} ({\ hat {E_ {j}}}) = \ delta _ {i, j} \ quad \ forall i, j = 1,2,3}$

где Кронекера функция. ${\ displaystyle \ delta}$

Преобразование опорного элемента

Для связывания опорного элемента с произвольным треугольником (вершинами :) используется линейное преобразование : ${\ displaystyle T}$${\ displaystyle E_ {1}, E_ {2}, E_ {3}}$ ${\ displaystyle F_ {T}}$

${\ displaystyle {\ begin {align} F_ {T} & \ двоеточие {\ hat {T}} \ to T, \ quad F (v) = B_ {T} v + b_ {T} \\ B_ {T} &: = \ left (E_ {2} -E_ {1}, E_ {3} -E_ {1} \ right), \ quad b_ {T}: = E_ {1}. \ end {align}}}$

Во многих задачах, связанных с уравнениями в частных производных , необходимо вычислить скалярное произведение базисных функций (определенных на любом треугольнике ): ${\ displaystyle L ^ {2}}$${\ displaystyle \ phi _ {я}}$${\ displaystyle T}$

${\ displaystyle (\ nabla \ phi _ {i}, \ nabla \ phi _ {j}) _ {L ^ {2} (T)} = \ int _ {T} \ nabla \ phi _ {i} (x ) \ cdot \ nabla \ phi _ {j} (x) dx.}$

С помощью набора трансформаций интегрирование можно перенести на опорный элемент:

${\ displaystyle \ int _ {T} \ nabla \ phi _ {i} (x) \ cdot \ nabla \ phi _ {j} (x) dx = \ int _ {\ hat {T}} \ left (\ left (DF_ {T} (z) \ right) ^ {- T} \ nabla {\ hat {\ phi}} _ {i} (z), \ left (DF_ {T} (z) \ right) ^ {- T} \ nabla {\ hat {\ phi}} _ {j} (z) \ right) _ {\ mathbb {R} ^ {2}} | \ det DF_ {T} (z) | dz.}$

литература

• Мартин Майр / Ульрих Тальхофер: Численные методы решения на практике: FEM-BEM-FDM . Hanser, 1993, ISBN 3-446-17061-8 , стр. 312 . 
• JN Reddy: Энергетические принципы и вариационные методы в прикладной механике . 2-е издание. John Wiley & Sons, 2002, ISBN 0-471-17985-X . 
• Д. Брэсс: теория конечных элементов, быстрые решатели и приложения в теории упругости . 4-е издание. Springer, 2007, ISBN 978-3-540-72449-0 . 
• Гюнтер Мюллер (ред.): FEM для практиков . 4 тома. Эксперт Верлаг, Реннинген. 
  • Том 1: Основы: базовые знания и рабочие примеры для приложений FEM. 2007, ISBN 978-3-8169-2685-6 .
  • Том 2: Структурная динамика. 2008, ISBN 978-3-8169-2842-3 .
  • Том 3: Температурные поля. 2007, ISBN 978-3-8169-2714-3 .
  • Том 4: Электротехника. 2009, ISBN 978-3-8169-2841-6 .
• Клаус-Юрген Бат: Методы конечных элементов . 2-е издание. Springer-Verlag, 2002, ISBN 3-540-66806-3 . 
• WE Gawehn: Метод конечных элементов . BOD Book on Demand, 2009, ISBN 978-3-8370-2497-5 (основы МКЭ для статики и динамики). 
• Франк Риг, Райнхард Хакеншмидт, Беттина Альбер-Лаукант: Анализ методом конечных элементов для инженеров: простое для понимания введение . Hanser Fachbuchverlag, 2012, ISBN 978-3-446-42776-1 (применение МКЭ в машиностроении). 
• Рене де Борст , Майк Крисфилд , Джорис Реммерс, Клеменс Верхусель: Нелинейный анализ твердых тел и конструкций методом конечных элементов , Wiley-VCH 2014
• Карл-Ойген Куррер : История теории структур. В поисках равновесия , Ernst and Son 2018, стр. 881–914, ISBN 978-3-433-03229-9

веб ссылки

• Метод конечных элементов в биомедицине, биомеханике и смежных областях.
• Численные методы (лекция и стажировка, сценарий) ( Памятка от 20 октября 2018 г. в Интернет-архиве )
• FU Mathiak: Метод конечных элементов (МКЭ). ( Памятка от 26 ноября 2019 г. в Интернет-архиве ) [PDF; 3,86 МБ].

Индивидуальные доказательства

1. ^ Карл Шельбах: Проблемы вариационного исчисления . В кн . : Журнал чистой и прикладной математики . Лента 41 , нет. 4 , 1852, стр. 293-363 . 
2. ↑ Эрнст Густав Кирш: Основные уравнения теории упругости твердых тел, выведенные из рассмотрения системы точек, соединенных упругими подпорками. В: Журнал Ассоциации немецких инженеров , том 7 (1868 г.), выпуск 8.
3. ^ Джон Уильям Стратт: По теории резонанса . В: Философские труды Лондонского королевского общества . Лента 161 , 1871, стр. 77-118 . 
4. ↑ Вальтер Ритц: О новом методе решения некоторых вариационных задач математической физики . В кн . : Журнал чистой и прикладной математики . Лента 135 , 1909, стр. 1-61 . 
5. ↑ Кристоф Хадерер: Исследования расширений и параметров одномерного стохастического конечно-элементного кода со случайными полями. Группа анализа инженерных рисков. Технический университет Мюнхена, 2017.
6. ^ Дэвид Ройланс: Анализ методом конечных элементов. (PDF; 348 kB), по состоянию на 10 мая 2017 г.