Круг Малфатти

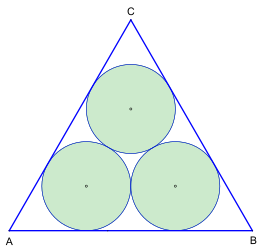
Три круга Малфатти , позже известные как проблема Мальфатти , названы в честь Джанфранческо Мальфатти , который заявил об их строительстве в 1803 году. В окружность мальфатти определяется - независимо от формы исходного треугольника - три кругов в треугольнике с тем свойством , что каждый затрагивает другие два круга с внешней стороны и две стороны треугольника с внутренней стороны .

Малфатти ошибочно предположил, что это свойство кругов решает проблему упаковки трех кругов в треугольник без перекрытия таким образом, чтобы они имели максимальную площадь . Почему круги Мальфатти не могут решить эту так называемую задачу максимизации Мальфатти , то есть максимальное покрытие треугольной области тремя кругами , можно увидеть, например, Б. легко узнать по длинному узкому прямоугольному треугольнику .

Следующее относится к радиусам окружностей Малфатти треугольника ABC:

${\ displaystyle r_ {A} = {\ frac {r} {2 (sa)}} (sr - ({\ overline {IB}} + {\ overline {IC}} - {\ overline {IA}})) }$

${\ displaystyle r_ {B} = {\ frac {r} {2 (sb)}} (sr - ({\ overline {IC}} + {\ overline {IA}} - {\ overline {IB}})) }$

${\ displaystyle r_ {C} = {\ frac {r} {2 (sc)}} (sr - ({\ overline {IA}} + {\ overline {IB}} - {\ overline {IC}})) }$

Он стоит за радиус вписанной и половину по окружности треугольника. это центр круга и три биссектрисы . ${\ displaystyle r}$${\ displaystyle s}$${\ displaystyle I}$${\ displaystyle \ omega _ {\ alpha}, \ omega _ {\ beta}, \ omega _ {\ gamma}}$

История

Задача о мраморе.
Треугольная призма с тремя вписанными цилиндрическими колоннами, а также девять возможных точек соприкосновения кругов Малфатти.

Первоначальная проблема Мальфатти была связана с проблемой стереотомии , предполагаемое решение которой Малфатти нашел в 1802 году и опубликовал в 1803 году в Memoria di Matematica e Fisica della Società Italiana delle Scienze в его статье Memoria sopra un проблема стереотомики . В начале своей статьи Мальфатти формулирует поставленную задачу.

В свободном переводе он гласит:

В случае прямоугольной треугольной призмы, изготовленной из любого материала, например мрамора, из нее вырезают три [круглых] цилиндра с той же высотой, что и призма, но с максимально возможным общим объемом, то есть с наименьшим возможным расходом материала в объеме призмы.

В своей статье « Memoria sopra un проблема стереотомики» Малфатти также указывает, что эту стереотомическую задачу можно свести к задаче геометрии поверхности. Он определяет положение кругов, вписанных в треугольник, который теперь называется кругами Малфатти, следующим образом:

Бесплатный перевод

Дан треугольник, постройте в нем три окружности так, чтобы каждая из окружностей касалась (то есть касалась точки) с двумя другими и с двумя сторонами треугольника.

Однако это было опровергнуто в 1992 г. В. А. Салгаллером и Г. А. Лос, которые показали, что решение вместо этого достигается путем нанесения круга с наибольшей площадью на последовательных этапах, описанных ниже в разделе построения согласно Салгаллеру и Лос .

Еще в 1687 году проблема построения Малфатти была решена Якобом I Бернулли в частном случае (равнобедренный треугольник), а позже Якоб Штайнер и Альфред Клебш дали решения чисто геометрическим способом , последний - с помощью эллиптических функций (1857, Crelle's Journal). Японец Адзима Наонобу также предложил решение за 30 лет до Малфатти в контексте японской архитектуры. То, что конструкция Малфатти не решает проблему Мальфатти во всех случаях, уже было показано Лобом и Ричмондом в 1930 году с помощью равносторонних треугольников и Говардом В. Ивсом в 1965 году с исследованиями с использованием узких и длинных треугольников. В 1967 году в эссе Майкла Голдберга даже было показано, что конструкция Малфатти никогда этого не делала. Как упоминалось выше, Салгаллер и Лос 1992 предоставили доказательства этого.

Геометрические конструкции

В 2003 году Ингмар Леманн объяснил различные решения проблемы Мальфатти в своем анализе Проблема Мальфатти - тема в продвижении одаренных студентов . Ниже подробно описаны четыре метода.

Строительство Малфатти

Круги Малфатти по Малфатти, расчетный эскиз

Вариант с предыдущими расчетами

С этой целью Леманн выводит три уравнения с помощью теоремы Пифагора и подобия треугольников , решения которых даются касательными отрезками и . ${\ displaystyle x \; = {\ overline {AC_ {1}}}, \; y = {\ overline {BC_ {2}}}}$${\ displaystyle z = {\ overline {CA_ {2}}}}$

Также учитываются следующие отношения:

${\ displaystyle {\ overline {AI}} = {\ sqrt {r ^ {2} + s ^ {2}}}, \; \; \; {\ overline {BI}} = {\ sqrt {r ^ { 2} + t ^ {2}}}, \; \; \; {\ overline {CI}} = {\ sqrt {r ^ {2} + u ^ {2}}},}$

здесь термины означают

${\ displaystyle s = {\ overline {AL_ {c}}}, \; t = {\ overline {BL_ {c}}}}$ и ${\ displaystyle u = {\ overline {CL_ {a}}}.}$

Используя соответствующие значения, теперь можно определить так называемую вспомогательную секцию${\ displaystyle {\ overline {PQ}}}$ длиной${\ displaystyle m}$

${\ displaystyle m = {\ frac {1} {2}} \ left ({\ overline {AI}} + {\ overline {BI}} + {\ overline {CI}} - {\ overline {AL_ {c}) }} - {\ overline {BL_ {c}}} - {\ overline {CL_ {a}}} + r \ right),}$

затем применяется к касательным участкам, описанным выше

${\ displaystyle x = {\ overline {AC_ {1}}} = {\ overline {AI}} - m, \; \; \; y = {\ overline {BC_ {2}}} = {\ overline {BI }} - m, \; \; \; z = {\ overline {CA_ {2}}} = {\ overline {CI}} - m.}$

Присваивается индивидуально слагаемым в формуле для множителя${\ displaystyle m}$${\ displaystyle {\ frac {1} {2}}}$

${\ displaystyle m = {\ frac {1} {2}} {\ overline {AI}} + {\ frac {1} {2}} {\ overline {BI}} + {\ frac {1} {2} } {\ overline {CI}} - {\ frac {1} {2}} {\ overline {AL_ {c}}} - {\ frac {1} {2}} {\ overline {BL_ {c}}} - {\ frac {1} {2}} {\ overline {CL_ {a}}} + {\ frac {1} {2}} r,}$

может быть отображена очень простая и компактная геометрическая конструкция (см. рисунок рядом).

Малфатти объезжает до Малфатти со строительством вспомогательного маршрута${\ displaystyle {\ overline {PQ}}}$

Описание конструкции

После рисования z. Б. неравными односторонний треугольник с длинами сторон и в центре вписанной окружности определяется с помощью три биссектрисы и . Это приводит к линии и Ниже сбрасывание перпендикуляра от на линию с базовой точкой и рисунок вписанной окружности вокруг с радиусом Падающего перпендикуляра от до к базовой точке и от до базовой точки , следующим образом . ${\ displaystyle ABC}$ ${\ displaystyle a, \; b}$${\ displaystyle c}$${\ displaystyle I}$${\ displaystyle \ omega _ {\ alpha}, \ omega _ {\ beta}}$${\ displaystyle \ omega _ {\ gamma}}$ ${\ displaystyle {\ overline {AI}}, {\ overline {BI}}}$${\ displaystyle {\ overline {CI}}.}$${\ displaystyle I}$${\ displaystyle {\ overline {BC}}}$${\ displaystyle L_ {a}}$${\ displaystyle k}$${\ displaystyle I}$ ${\ displaystyle {\ overline {IL_ {a}}}.}$${\ displaystyle I}$${\ displaystyle {\ overline {AC}}}$${\ displaystyle L_ {b}}$${\ displaystyle I}$${\ displaystyle {\ overline {AB}}}$${\ displaystyle L_ {c}}$

Теперь длина вспомогательного маршрута определяется по прямой следующим образом . Сначала дорожка делится пополам и складывается из суммы половин дорожки, и, наконец, вычитается и добавляется полученная половина остатка Inkreisradius . ${\ displaystyle m}$${\ displaystyle {\ overline {PQ}}}$${\ displaystyle {\ frac {1} {2}} {\ overline {AI}}, \; {\ frac {1} {2}} {\ overline {BI}}}$${\ displaystyle {\ frac {1} {2}} {\ overline {CI}}}$${\ displaystyle {\ frac {1} {2}} {\ overline {AL_ {c}}}, \; {\ frac {1} {2}} {\ overline {BL_ {c}}}}$${\ displaystyle {\ frac {1} {2}} {\ overline {CL_ {a}}}}$${\ displaystyle {\ frac {1} {2}} r}$

Он продолжается определением центров кругов Малфатти. Другими словами, коснитесь вспомогательной секции циркулем и перенесите ее на три биссектрисы и от центра вписанного круга ; это приводит к точкам и от точек и с дуги вверх в сторону треугольника и от дуги до и включая точки и следует , возведение трех перпендикуляров от базовых точек и на соответствующей отрезке и , таким образом , искомые точек центра и результата${\ displaystyle {\ overline {PQ}},}$${\ displaystyle m,}$${\ displaystyle \ omega _ {\ alpha}, \ omega _ {\ beta}}$${\ displaystyle \ omega _ {\ gamma}}$${\ displaystyle I}$${\ Displaystyle D, \; E}$${\ displaystyle F.}$${\ displaystyle D}$${\ displaystyle E}$${\ displaystyle c}$${\ displaystyle F}$${\ displaystyle a}$${\ Displaystyle C_ {1}, \; C_ {2}}$${\ displaystyle A_ {2}.}$${\ Displaystyle C_ {1}, \; C_ {2}}$${\ displaystyle A_ {2}}$${\ displaystyle \ omega _ {\ alpha}, \ omega _ {\ beta}}$${\ displaystyle \ omega _ {\ gamma};,}$${\ Displaystyle M_ {A}, \; M_ {B}}$${\ displaystyle M_ {C}.}$

Чтобы получить точки соприкосновения и три отвеса должен быть вырублен из центральных точек и на стороны треугольника и снова . И, наконец, привлечь к Малфатти кругов и с радиусами и и вы получите свою последнюю три точки соприкосновения и${\ Displaystyle B_ {2}, \; A_ {1}}$${\ displaystyle B_ {1}}$${\ Displaystyle M_ {A}, \; M_ {B}}$${\ displaystyle M_ {C}}$${\ Displaystyle б, \; а}$${\ displaystyle b}$${\ displaystyle k_ {A}, \; k_ {B}}$${\ displaystyle k_ {C}}$${\ Displaystyle r_ {A}, \; r_ {B}}$${\ displaystyle r_ {C}}$${\ Displaystyle G, \; H}$${\ displaystyle J.}$

Таким образом , три Малфаттей кругов и их девять возможных точек соприкосновения и построены. ${\ displaystyle k_ {A}, \; k_ {B}}$${\ displaystyle k_ {C}}$${\ Displaystyle C_ {1}, \; C_ {2}, \; A_ {1}, \; A_ {2}, \; B_ {1}, \; B_ {2}, \; G, \; H. }$${\ displaystyle J}$

Строительство по Штайнеру-Петерсену

В 1826 году Якоб Штайнер связал круги Мальфатти с вписанными окружностями, состоящими из трех подтреугольников, которые, следовательно, можно использовать в качестве конструктивного элемента для кругов Мальфатти. Штайнер сформулировал следующее предложение:

Здесь следует подчеркнуть, что касательные к окружностям Малфатти, упомянутые Штайнером, обычно являются не биссектрисами , а их зеркальным отображением на прямых линиях, соединяющих два центра вписанных окружностей частичных треугольников. ${\ Displaystyle \ треугольник ABC}$

В 1879 году Юлиус Петерсен нашел элементарное геометрическое решение (вариант без предварительных вычислений) конструкционной задачи Малфатти, которая показана ниже.

Описание конструкции

Для ясности целесообразно показать конструкцию в трех основных этапах (1) - (3). Только соответствующие элементы конструкции переносятся с первой на вторую или со второй на третью главную ступеньку.

Окружности Малфатти по Штайнеру-Петерсену
(1) Главный шаг: построение трех вписанных окружностей частичных треугольников и${\ Displaystyle \ треугольник BCI, \; \ треугольник CAI}$${\ Displaystyle \ треугольник ABI}$

(1) Построение трех вписанных окружностей частичных треугольников и${\ Displaystyle \ треугольник BCI, \; \ треугольник CAI}$${\ Displaystyle \ треугольник ABI.}$

После нанесения z. B. Неравномерный треугольник с длинами сторон и центром вписанной окружности определяется с помощью трех биссектрис и . Inkreismittelpunkte и суб-треугольники и снова получаются как пересечение двух биссектрис, г. Б. путем деления углов на четыре части и. Он следует за падением перпендикуляра на линию с базовой точкой и рисованием вписанного круга вокруг с радиусом. Вырубка перпендикуляра сверху до базовой точки и от верхней точки до базовой точки и нанесение двух последних вписанный и вокруг их середин или связаны. ${\ displaystyle ABC}$${\ displaystyle a, \; b}$${\ displaystyle c}$${\ displaystyle I}$${\ displaystyle \ omega _ {\ alpha}, \ omega _ {\ beta}}$${\ displaystyle \ omega _ {\ gamma}}$${\ Displaystyle M_ {P}, \; M_ {Q}}$${\ displaystyle M_ {R}}$${\ Displaystyle \ треугольник BCI, \; \ треугольник CAI}$${\ Displaystyle \ треугольник ABI}$${\ Displaystyle \ альфа, \; \ бета,}$${\ displaystyle \ gamma.}$${\ displaystyle M_ {P}}$${\ displaystyle {\ overline {BC}}}$${\ displaystyle P}$${\ displaystyle k_ {P}}$${\ displaystyle M_ {P}}$${\ displaystyle {\ overline {M_ {P} P}}.}$${\ displaystyle M_ {Q}}$${\ displaystyle {\ overline {AC}}}$${\ displaystyle Q}$${\ displaystyle M_ {R}}$${\ displaystyle {\ overline {AB}}}$${\ displaystyle R}$${\ displaystyle k_ {Q}}$${\ displaystyle k_ {R},}$${\ displaystyle M_ {Q}}$${\ displaystyle M_ {R},}$

Окружности Малфатти по Штайнеру-Петерсену
(2) основной шаг: построение трех касательных и${\ displaystyle {\ overline {RZ}}, {\ overline {PX}}}$${\ displaystyle {\ overline {QY}}}$

(2) Построение трех касательных и${\ displaystyle {\ overline {RZ}}, {\ overline {PX}}}$${\ displaystyle {\ overline {QY}}}$

Он по- прежнему с соединительными точками с биссекторным след в и рисунке в Thales круга Он разрежет вписанную окружность в точках и в настоящее время привлекает вас в первую касательной от точки через точку , где вписанный круг , пока они не достигают стороны треугольника в разрезах. ${\ displaystyle R}$${\ displaystyle M_ {P},}$${\ displaystyle {\ overline {RM_ {P}}}}$${\ displaystyle M_ {1}}$ ${\ displaystyle k_ {1}.}$${\ displaystyle k_ {P}}$${\ displaystyle K}$${\ displaystyle L.}$${\ displaystyle R}$${\ displaystyle L}$${\ displaystyle k_ {P},}$${\ displaystyle b}$${\ displaystyle Z}$

После этого, с маршрутом , подключенным в Половинках и окружностями долин расположены. Он разрежет вписанную окружность в точках и на прорисовку второй касательной от точки через , пока они не достигают стороны треугольника в разрезах, обеспечивает пересечение С точкой на третьей касательной должно быть, она требует для своего определения лишь линия от до сторона треугольника и точка пересечения, таким образом определяется и третья касательная . ${\ displaystyle P}$${\ displaystyle M_ {Q}}$${\ displaystyle {\ overline {PM_ {Q}}}}$${\ displaystyle M_ {2}}$${\ displaystyle k_ {2}}$${\ displaystyle k_ {Q}}$${\ displaystyle O}$${\ displaystyle N.}$${\ displaystyle P}$${\ displaystyle N,}$${\ displaystyle b}$${\ displaystyle X}$${\ displaystyle T.}$${\ displaystyle T}$${\ displaystyle Q}$${\ displaystyle T}$${\ displaystyle c}$${\ displaystyle Y.}$${\ displaystyle {\ overline {QY}}}$

Круги Малфатти по Штайнеру-Петерсену
(3) основной шаг: построение кругов Малфатти и${\ displaystyle k_ {A}, k_ {B}}$${\ displaystyle k_ {C}}$

(3) Построение кругов Малфатти и${\ displaystyle k_ {A}, \; k_ {B}}$${\ displaystyle k_ {C}}$

Сначала в треугольнике проводится биссектриса от точки к биссектрисе ; это приводит к центру первого круга Малфатти. За этим следует опуская перпендикуляр из на линию с базовой точкой и рисунком первого Малфатти круг вокруг с радиусом. Валок перпендикуляра сверху , чтобы с базовой точкой и от касательной к базовой точке следующим образом . Следующая строка вниз через биссектрису создает центральную точку. После того , как второй Малфатти круг был составлен в с радиусом , перпендикуляры вырезаны из вверх с базовой точкой из вверх с базовой точкой и от по касательному с базовой точкой . В следующей строке вниз по биссектрисе создает центральную точку. Теперь третий Малфатти круг рисуется вокруг с радиусом${\ displaystyle ARZ}$${\ displaystyle \ omega _ {\ epsilon}}$${\ displaystyle R}$${\ displaystyle \ omega _ {\ alpha}}$${\ displaystyle M_ {A}}$${\ displaystyle M_ {A}}$${\ displaystyle {\ overline {AB}}}$${\ displaystyle C_ {1}}$${\ displaystyle k_ {A}}$${\ displaystyle M_ {A}}$${\ displaystyle {\ overline {M_ {A} C_ {1}}}.}$${\ displaystyle M_ {A}}$${\ displaystyle {\ overline {AC}}}$${\ displaystyle B_ {2}}$${\ displaystyle M_ {A}}$${\ displaystyle RZ}$${\ displaystyle C '}$${\ displaystyle M_ {A}}$${\ displaystyle C '}$${\ displaystyle \ omega _ {\ beta}}$${\ displaystyle M_ {B}.}$${\ displaystyle k_ {B}}$${\ displaystyle M_ {B}}$${\ displaystyle {\ overline {M_ {B} C '}}}$${\ displaystyle M_ {B}}$${\ displaystyle {\ overline {AB}}}$${\ displaystyle C_ {2},}$${\ displaystyle M_ {B}}$${\ displaystyle {\ overline {BC}}}$${\ displaystyle A_ {1}}$${\ displaystyle M_ {B}}$${\ displaystyle PX}$${\ displaystyle A '}$${\ displaystyle M_ {B}}$${\ displaystyle A '}$${\ displaystyle \ omega _ {\ gamma}}$${\ displaystyle M_ {C}.}$${\ displaystyle k_ {C}}$${\ displaystyle M_ {C}}$${\ displaystyle {\ overline {M_ {C} A '}}.}$

В точках соприкосновения , и для получения, он по- прежнему требует два припоев осажденных из центра на из на и связи точки с${\ Displaystyle A_ {2}, \; B_ {1}}$${\ displaystyle B '}$${\ displaystyle M_ {C}}$${\ displaystyle {\ overline {BC}},}$${\ displaystyle M_ {C}}$${\ displaystyle {\ overline {AC}}}$${\ displaystyle M_ {A}}$${\ displaystyle M_ {C}.}$

Таким образом , три Малфаттей кругов и их девять возможных точек соприкосновения и построены. ${\ displaystyle k_ {A}, \; k_ {B}}$${\ displaystyle k_ {C}}$${\ Displaystyle C_ {1}, \; C_ {2}, \; A_ {1}, \; A_ {2}, \; B_ {1}, \; B_ {2}, \; A ', \; B '}$${\ displaystyle C '}$

Строительство по Лобу и Ричмонду

Построение по Х. Лобу и Х. У. Ричмонду
равностороннего треугольника с вписанной окружностью как часть решения задачи максимизации

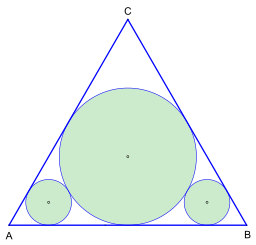
Х. Лоб и Х. У. Ричмонд опубликовали решение проблемы максимизации Малфатти в 1930 году. Вписанный круг равностороннего треугольника используется как круг из трех. Покрытие треугольной области таким расположением кругов лишь незначительно больше, а именно на , но задача проста и может быть представлена ​​без особых усилий. ${\ Displaystyle \ приблизительно 1 \, \%}$

Вы доказали

Описание конструкции

После построения равностороннего треугольника со сторонами равной длины и центр вписанной окружности определяется с помощью трех биссектрис и . Затем следует падение перпендикуляра к линии с базовой точкой и рисование вписанной окружности вокруг радиуса, точки пересечения с биссектрисой и с биссектрисой. Палить перпендикуляр сверху до базовой точки и от верхней до базовой точки следует. . ${\ displaystyle ABC}$${\ displaystyle a, \; b}$${\ displaystyle c}$${\ displaystyle I}$${\ displaystyle \ omega _ {\ alpha}, \ omega _ {\ beta}}$${\ displaystyle \ omega _ {\ gamma}}$${\ displaystyle I}$${\ displaystyle {\ overline {BC}}}$${\ displaystyle D}$${\ displaystyle k}$${\ displaystyle I}$${\ displaystyle {\ overline {ID}};}$${\ displaystyle E}$${\ displaystyle \ omega _ {\ alpha}}$${\ displaystyle F}$${\ displaystyle \ omega _ {\ beta}.}$${\ displaystyle I}$${\ displaystyle {\ overline {AC}}}$${\ displaystyle G}$${\ displaystyle I}$${\ displaystyle {\ overline {AB}}}$${\ displaystyle H}$

Для меньших кругов вы проводите две параллели прямой (в равностороннем треугольнике)  - одну от точки до линии с пересечением , вторую от точки до линии с пересечением . Установление перпендикуляра с основанием на биссектрисе. и установка перпендикуляра на биссектрисе с базовой точкой приводит к получению центральных точек, и теперь круг рисуется с радиусом, а круг вокруг радиуса . Чтобы получить последние две точки соприкосновения, затем наваливаются два отвеса , от и от , в результате чего получаются базовые точки и${\ displaystyle {\ overline {AB}}}$${\ displaystyle E}$${\ displaystyle {\ overline {AC}}}$${\ displaystyle J}$${\ displaystyle F}$${\ displaystyle {\ overline {BC}}}$${\ displaystyle K.}$${\ displaystyle J}$${\ displaystyle \ omega _ {\ alpha}}$${\ displaystyle \ omega _ {\ beta}}$${\ displaystyle K}$${\ displaystyle M_ {A}}$${\ displaystyle M_ {B}.}$${\ displaystyle M_ {A}}$${\ displaystyle {\ overline {M_ {A} E}}}$${\ displaystyle M_ {B}}$${\ displaystyle {\ overline {M_ {B} F}}}$${\ displaystyle {\ overline {AB}}}$${\ displaystyle M_ {A}}$${\ displaystyle M_ {B}}$${\ displaystyle L}$${\ displaystyle M.}$

Таким образом, три круга и с их девяти возможных точек соприкосновения и построены в равносторонний треугольник . ${\ displaystyle k, \; k_ {A}}$${\ displaystyle k_ {B}}$${\ Displaystyle D, \; E, \; F, \; G, \; H, \; J, \; K, \; L}$${\ displaystyle M}$

Строительство Гольдберга

Майкл Голдберг опубликовал в 1967 году эссе, в котором показал, что конструкция Малфатти, независимо от формы треугольника, никоим образом не может удовлетворить задачу максимизации. Он пришел к этому результату - не доказав его - посредством исследований с использованием треугольников различной формы, которые все имели одну общую черту: один из трех кругов всегда был вписанным кругом.

Описание конструкции

Построение по Голдбергу, общий треугольник с вписанной окружностью как одна из трех окружностей, решающих задачу максимизации.
Радиус из этого следует: Третий круг лежит на биссектрисе.${\ displaystyle {\ overline {SR}} <{\ overline {OM}},}$${\ displaystyle \ omega _ {\ alpha}.}$

После рисования неправильного треугольника центр вписанной окружности определяется с помощью двух биссектрис и . Это приводит к валентному и сопровождаются осаждением припоя расстояния до точки стопы и рисунка вписанной окружности к радиусу от точки пересечения на это в случае, припои на с базовой точкой , а также на чтобы точка стопы включает в себе . ${\ displaystyle ABC}$${\ displaystyle I}$${\ displaystyle \ omega _ {\ alpha}}$${\ displaystyle \ omega _ {\ gamma}}$${\ displaystyle {\ overline {AI}}}$${\ displaystyle {\ overline {CI}}.}$${\ displaystyle I}$${\ displaystyle {\ overline {AB}}}$${\ displaystyle D}$${\ displaystyle I}$${\ displaystyle {\ overline {ID}};}$${\ displaystyle \ omega _ {\ alpha}}$${\ displaystyle E.}$${\ displaystyle I}$${\ displaystyle {\ overline {AC}}}$${\ displaystyle F}$${\ displaystyle I}$${\ displaystyle {\ overline {BC}}}$${\ displaystyle G}$

Центр второго круга теперь очень легко определяется в два этапа. Существует необходимость только в перпендикулярной траекторию от точки к в разрезах, а биссектриса угла , полученной таким образом точка является центр второй окружности с радиусом и контактными точками и с двух сторон треугольника. ${\ displaystyle {\ overline {AI}}}$${\ displaystyle E,}$${\ displaystyle {\ overline {AC}}}$${\ displaystyle H}$${\ displaystyle AHE.}$${\ displaystyle J}$${\ displaystyle {\ overline {JE}}}$${\ displaystyle K}$${\ displaystyle L}$

Чтобы найти наибольший возможный радиус для третьей и последней искомой окружности, возможные радиусы сначала определяются по двум биссектрисам - по трем, если этого требует форма треугольника. Он получается аналогичным повторением этапов построения второй окружности с центром.Пунктирные линии на соседнем рисунке показывают радиус, построенный по биссектрисе, в сравнении с радиусом . Результатом оценки двух радиусов . Из этого следует: окружность вокруг центра - это максимально возможный третий искомый круг. ${\ displaystyle J.}$${\ displaystyle \ omega _ {\ beta}}$${\ displaystyle {\ overline {SR}},}$${\ displaystyle {\ overline {OM}}}$${\ displaystyle \ omega _ {\ alpha}.}$${\ displaystyle {\ overline {SR}} <{\ overline {OM}}}$${\ displaystyle O}$

Строительство по Салгаллеру и Лос

У. А. Салгаллер и Г. А. Лос опубликовали - после своего доказательства в 1992 г. (см. Историю ) - в 1994 г. в Journal of Mathematical Sciences свое решение проблемы максимизации Малфатти. Есть ты. а. Можно увидеть пять общих треугольников, в каждый из которых вписанный круг является одним из трех неперекрывающихся кругов. Только в его треугольнике, описанном в конструкции по Голдбергу , эти три окружности лежат на одной биссектрисе.

Бесплатный перевод

Треугольник покрыт тремя кругами

• Метод Мальфатти (рис. 1) и метод Штайнера-Петерсена были достигнуты

${\ displaystyle \ left ({\ sqrt {3}} - {\ frac {3} {2}} \ right) \ cdot \ pi \ приблизительно 0 {,} 72910}$ или ок. ${\ displaystyle 72 {,} 91 \, \%.}$

• Метод по Лобу и Ричмонду (рис. 2) позволил получить

${\ displaystyle {\ frac {11 {\ sqrt {3}}} {81}} \ cdot \ pi \ приблизительно 0 {,} 73895}$ или ок. ${\ displaystyle 73 {,} 90 \, \%.}$

• Метод с вписанной окружностью по Салгаллеру и Лосу, а также метод по Голдбергу (рисунок 3 и рисунок 4):

Покрытие треугольной области, например B. в виде процентного значения выбранной формы выходного треугольника, а также положения кружков и зависимых. Для показанных фигур с соответствующими областями применяется формула процента:${\ displaystyle k_ {2}}$${\ displaystyle k_ {3}}$${\ displaystyle A}$

${\ Displaystyle {\ frac {A_ {k_ {1}} + A_ {k_ {2}} + A_ {k_ {3}}} {A {_ {\ треугольник {ABC}}}}} \ cdot 100 \, \%,}$

это приводит к покрытию треугольной области для треугольника на рисунке 3 или для треугольника на рисунке 4${\ Displaystyle \ приблизительно 72 {,} 70 \; \%}$${\ Displaystyle \ приблизительно 77 {,} 1 \; \%.}$

• 

  Рисунок 1: Метод Малфатти и метод Штайнера-Петерсена в равностороннем треугольнике, покрывающем площадь треугольника около 72,91%.

• 

  Рисунок 2: Метод по Лобу и Ричмонду в равностороннем треугольнике, охват треугольной области около 73,90%

• 

  Рис. 3: Метод Салгаллера и Лоса, а также метод Гольдберга с вписанным кругом ; в показанном виде охват треугольной области составляет примерно 72,70%. ${\ displaystyle k_ {1}}$

• 

  Рис. 4: Метод Салгаллера и Лоса, а также метод Гольдберга с вписанным кругом ; в показанном виде охват треугольной области составляет около 77,1%. ${\ displaystyle k_ {1}}$

литература

• Курт Лёбер: Вклад в решение и историю проблемы Мальфатти и ее расширений. Вступительная диссертация. SUB Геттингене, Гёттинген Оцифровка центр, 1914, доступ к 4 октября 2020 года . 
• Марко Андреатта, Андрас Бездек, Ян П. Боронски: Проблема Мальфатти: два столетия споров , Mathematical Intelligencer, 2011, № 1.
• Генрих Дёрри : проблема Малфатти в 100 великих проблемах элементарной математики: их история и решения . Довер, Нью-Йорк, 1965, ISBN 0-486-61348-8 , стр. 147-151.
• Майкл Голдберг: Об исходной задаче Малфатти в математике, журнал № 40, 1967, стр. 241-247.
• Чарльз Стэнли Огилви: Экскурсии по геометрии . Довер, Нью-Йорк, 1990, ISBN 0-486-26530-7 .
• В. А. Салгаллер, Г. А. Лос: Решение проблемы Мальфатти . В: Журнал математических наук . 72, No. 4, 1994, pp. 3163-3177.

веб ссылки

• Эрик В. Вайсштейн : Круги Малфатти . В: MathWorld (английский).
• Эрик В. Вайсштейн : Проблема Малфатти . В: MathWorld (английский).
• Проблема Малфатти. В: Разрежьте узел. Проверено 4 октября 2020 года . 

Индивидуальные доказательства

1. ↑ Курт Лёбер: Исторический обзор (введение). В: Вклад в решение и историю проблемы Мальфата и ее расширений. SUB Гёттинген, Götinger Оцифровка центр, 1914, стр. 1 , доступ к 15 ноября 2020 года . 
2. ↑ Джанфранческо Мальфатти: Memoria sopra un проблема стереотомики , Memorie di Matematica e Fisica della Società Italiana delle Scienze, No. 10, 1, 1803, pp. 235–244, по состоянию на 15 ноября 2020 г.
3. ↑ Джанфранческо Мальфатти: Memoria sopra un проблема стереотомики , Memorie di Matematica e Fisica della Società Italiana delle Scienze, No. 10, 1, 1803, p. 243 ff, по состоянию на 15 ноября 2020 г.
4. ↑ ^{a b} Ингмар Леманн: 1. История Мальфатти, стр. 1. (PDF) В: Проблема Мальфатти - тема продвижения талантливых людей. TU Dortmund University, 2003, доступ к 19 ноября 2020 года . 
5. ↑ ^{a b c d} Ингмар Леманн: 1. История Мальфатти, страница 2. (PDF) В: Проблема Мальфатти - тема поощрения талантливых студентов. TU Dortmund University, 2003, доступ на 7 ноября 2020 года . 
6. ↑ ^{a b c d} Рауль Ибаньес: El проблема Мальфатти. culturacientifica, Matemoción, 5 апреля 2017 г., по состоянию на 5 октября 2018 г. (испанский). 
7. ↑ ^{a b c} Sic! - Согласно правилам транскрипции немецкоязычной Википедии (сноска 6) , это написание Los отличается от написания Los ' (с апострофом), которое в основном встречается в других местах . Б. тоже здесь.
8. ↑ ^{а б в г} Ингмар Леманн: Построение кругов Малфатти, стр. 3–5. (PDF; 143 КБ) В: Проблема Мальфатти - Тема в продвижении одаренных, 15 страниц. TU Dortmund University, 2003, доступ к 4 октября 2020 года . 
9. ↑ ^{a b} Курт Лёбер: Исторический обзор (введение). В: Вклад в решение и историю проблемы Мальфата и ее расширений. SUB Гёттинген, Götinger Оцифровка центр, 1914, стр. 2 сл. , Accessed 4 октября 2020 года . 
10. ^ Жак Бернулли: Oeuvres Complete, Женева 1744 г., Том 1, стр.303.
11. ↑ Якоб Штайнер: Некоторые геометрические утверждения ; Gesammelte Werke Якоба Штайнера, том 1, Г. Реймер, 1881 г., стр. 3, в поиске книг Google, по состоянию на 15 ноября 2020 г.
12. ↑ Якоб Штайнер: Некоторые геометрические соображения ; Gesammelte Werke Якоба Штайнера, том 1, Г. Реймер, 1881, стр. 19, в поиске книг Google, по состоянию на 15 ноября 2020 г.
13. ^ Альфред Клебш: Применение эллиптических функций к проблеме геометрии пространства. В: Журнал теоретической и прикладной математики (журнал Crelle в), Том 53. SUB Гёттинген, Götinger Оцифровка центр, 1857, . С. 292-308 , доступ к 15 ноября 2020 года . 
14. ^ Аджима Наонобу в своей основной работе Fukyo Сампо из 1799 Джон Дж О'Коннор, Эдмунд Ф. Робертсон :  Малфатти круг. В: Архив истории математики MacTutor .
15. ^ ^{A b} Х. Лоб, HW Ричмонд: О решениях проблемы Малфатти для треугольника. (PDF) Лондонское математическое общество, 1930, доступ к 20 ноября 2020 . 
16. ↑ ^{a b} Майкл Голдберг: Об исходной проблеме Мальфатти . В: Атлантический университет Флориды (ред.): Математический журнал . лента 40 , нет. 5 , ноябрь 1967, стр. 241-247 , JSTOR : 2688277 ( Об исходной задаче Мальфатти [PDF; по состоянию на 20 ноября 2020 г.]). 
17. ↑ Ингмар Леманн: Строительство по Штайнер-Петерсену, стр. 5. (PDF) В: Проблема Мальфатти - тема поощрения одаренных студентов. TU Dortmund University, 2003, доступ к 2 октября 2018 года . 
18. ↑ Юлиус Петерсен, Р. фон Фишер-Бензон (Überstzer): Методы и теории решения задач геометрического построения. В: Konstruktionsaufgabe 404. Мичиганского университета, библиотека, 1879 г., . С. 102-104 , доступ к 15 ноября 2020 года . 
19. ↑ ^{a b} Ингмар Леманн: Строительство по Штайнер-Петерсену, стр. 8 и сл. (PDF) В: Проблема Мальфатти - тема поощрения талантливых студентов. TU Dortmund University, 2003, доступ к 2 октября 2018 года . 
20. ↑ Sic! - Это написание Salgaller соответствует Wikipedia: соглашения об именах , см. Также Wiktor Abramowitsch Salgaller
21. ↑ ^{а б} В. А. Салгаллер, Г. А. Лос: Решение проблемы Малфатти . В: Журнал математических наук . 72, № 4, 1994, стр.  3163 и далее, рис. 1, Springer Link, PDF . Проверено 5 октября, 2020.
22. ↑ Хайме Рангель-Мондрагон: Проблема Мальфатти. (PDF) В: Демонстрационный проект Вольфрама. Вольфрам, 2011, доступ к 24 ноября 2020 . 
23. ^ Arnold Math Jn: 2.2 Решение проблемы мрамора Малфатти. (PDF) В: О проблеме Малфатти с мрамором. Институт математических наук, Stony Brook University, Нью - Йорк, июнь 2016, доступ к 24 ноября 2020 . 

Эта статья была добавлена в список отличных статей данной версии 25 ноября 2020 года .