Поверхность революции

Вращение дуги cos (см. Ниже)

Тор как поверхность вращения

Поверхность вращения или поверхность вращения находится в геометрии на поверхности , определяемой вращением плоской кривой, от главного меридиана , на лежащих в одной плоскости линии, ось вращения , формируется. Простой пример - прямой круговой конус. Он создается путем вращения прямой линии вокруг оси вращения, которая ее пересекает. Другие простые примеры: прямой круговой цилиндр (вращение прямой линии вокруг оси, параллельной ей), сфера (вращение окружности вокруг диаметра) и тор (вращение окружности, не пересекающей ось). Поверхности вращения обладают особыми свойствами по сравнению с другими поверхностями:

• Поверхности вращения являются вращательно-симметричными , т.е. основная геометрическая информация уже содержится в главном меридиане. Поэтому они имеют относительно простые аналитические описания .
• Сечение с любой плоскостью, содержащей ось вращения, называется меридианом и всегда совпадает с главным меридианом.
• Поперечное сечение, т.е. ЧАС. Плоское сечение с плоскостью, перпендикулярной оси вращения, всегда является кругом и называется кругом широты .
• Меридианы и параллели - это линии кривизны поверхности вращения . (Они пересекаются перпендикулярно и указывают направления максимальной и минимальной нормальной кривизны в каждой точке (см. Тор).)

Дополнительные примеры: эллипсоид вращения , параболоид вращения , гиперболоид вращения .

Комментарий:

1. Поверхность вращения также можно создать, вращая другую подходящую кривую, которая не находится в той же плоскости, что и ось вращения. Простой пример - гиперболоид вращения. Его можно создать, вращая лежащую на нем прямую (наклоненную к оси вращения). Образующая прямая не является меридианом.
2. Контур поверхности вращения , как правило , не является меридиан или другое плоским сечение, см конструкции контура .

Аналитические описания

Вращение точки

Аналитическое описание поверхности вращения напрямую зависит от аналитического описания повернутой плоской кривой, главного меридиана. В дальнейшем всегда предполагается, что ось z является осью вращения .

Если вы позволите точке плоскости xz вращаться вокруг оси z, вы получите круг с радиусом . ${\ displaystyle (r_ {0}, 0, z_ {0}), \ r_ {0} \ geq 0}$${\ displaystyle (r_ {0} \ cos \ varphi, r_ {0} \ sin \ varphi, z_ {0}), \ 0 \ leq \ varphi <2 \ pi \,}$${\ displaystyle r_ {0}}$

Меридиан в параметрической форме

Конус как поверхность вращения

Эллипсоид как поверхность вращения

В этом случае предполагается, что

• главный меридиан - кривая с .${\ displaystyle m_ {0}}$${\ Displaystyle (г (т), 0, г (т)), \ t_ {1} \ leq t \ leq t_ {2}}$${\ Displaystyle г (т) \ geq 0}$

Тогда параметрическая форма соответствующей поверхности вращения равна

• ${\ Displaystyle (р (т) \ соз \ варфи, р (т) \ грех \ варфи, г (т)), \ \ т_ {1} \ leq t \ leq t_ {2}, 0 \ leq \ varphi < 2 \ пи \.}$

По геометрическим соображениям обычно важно иметь нормаль к поверхности. При соответствующих условиях дифференцируемости это приводит к нормали к поверхности в точке${\ Displaystyle (г \ соз \ varphi, г \ грех \ varphi, z) \:}$

• ${\ displaystyle {\ vec {n}} = ({\ dot {z}} \ cos \ varphi, {\ dot {z}} \ sin \ varphi, - {\ dot {r}}) \.}$

Для результатов по площади поверхности (без возможных нижних и верхних кружков!)

${\ displaystyle A = 2 \ pi \ int _ {t_ {1}} ^ {t_ {2}} r \ {\ sqrt {{\ dot {r}} ^ {2} + {\ dot {z}} ^ {2}}} \, dt,}$.

Примеры:

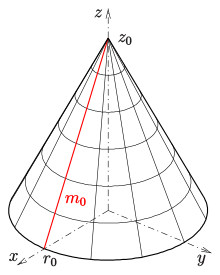
1) (расстояние) дает конус${\ displaystyle m_ {0} :( r_ {0} t, 0, z_ {0} (1-t)), \ 0 \ leq t \ leq 1}$

${\ displaystyle (r_ {0} t \ cos \ varphi, r_ {0} t \ sin \ varphi, z_ {0} (1-t), \ \ 0 \ leq t \ leq 1.0 \ leq \ varphi <2 \ число Пи \,}$

с радиусом и высотой базовой окружности .${\ displaystyle r_ {0}}$${\ displaystyle z_ {0}}$

2) (кружок) дает тор (см. Рисунок) ${\ displaystyle m_ {0} :( R + a \ cos t, 0, a \ sin t), \ 0 \ leq t \ leq 2 \ pi, \ R> a}$

${\ Displaystyle ((р + а \ соз т) \ соз \ varphi, (р + а \ соз т) \ грех \ варфи, а \ грех т), \ 0 \ leq т \ leq 1.0 \ leq \ varphi <2 \ число Пи \.}$

3) (полуэллипс) дает эллипсоид вращения${\ displaystyle m_ {0} :( a \ cos t, 0, b \ sin t), \ 0 \ leq t \ leq \ pi, \}$

${\ Displaystyle (а \ соз т \ соз \ варфи, а \ соз т \ грех \ варфи, б \ грех т) \ 0 \ Leq т \ Leq \ пи, \ 0 \ leq \ varphi <2 \ пи \.}$

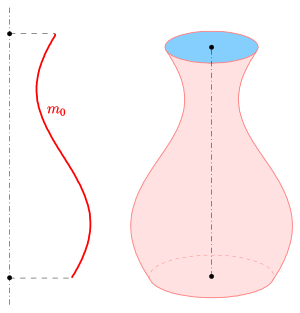
4) (косинусная кривая) результаты ${\ displaystyle m_ {0} :( a \ cos 2 \ pi {\ tfrac {tb} {l}} + c, 0, t), \ 0 \ leq t \ leq h, \}$

${\ displaystyle \ left ((a \ cos 2 \ pi {\ tfrac {tb} {l}} + c) \ cos \ varphi, (a \ cos 2 \ pi {\ tfrac {tb} {l}} + c ) \ sin \ varphi, t \ right) \ 0 \ leq t \ leq h, \ 0 \ leq \ varphi <2 \ pi \.}$

Для первой картины (вазы) использовались следующие параметры:

${\ displaystyle a = 10, b = 20, l = 100, c = 20, h = 90}$

Меридиан в неявной форме

Поверхность вращения, меридиан = кривая Кассини

В этом случае предполагается, что

• главный меридиан - это кривая, неявно заданная в плоскости rz уравнением с .${\ displaystyle m_ {0}}$${\ displaystyle f (r, z) = 0}$${\ displaystyle r \ geq 0}$

Неявное представление связанной поверхности вращения является результатом замены ${\ displaystyle r = {\ sqrt {x ^ {2} + y ^ {2}}} \:}$

• ${\ displaystyle f ({\ sqrt {x ^ {2} + y ^ {2}}}, z) = 0 \.}$

Нормаль к поверхности в точке поверхности : ${\ Displaystyle (Икс, Y, Z) = (г \ соз \ varphi, г \ грех \ varphi, z)}$

• ${\ displaystyle {\ vec {n}} = (f_ {r} \ cos \ varphi, f_ {r} \ sin \ varphi, f_ {z}) \.}$

Примеры:

1) (расстояние) дает конус с уравнением ${\ displaystyle m_ {0}: z_ {0} r + r_ {0} z-r_ {0} z_ {0} = 0, \ r_ {0}, z_ {0}> 0, \ 0 \ leq r \ leq r_ {0} \,}$

${\ displaystyle z_ {0} ^ {2} (x ^ {2} + y ^ {2}) = r_ {0} ^ {2} (z_ {0} -z) ^ {2} \,}$радиус и высота базовой окружности .${\ displaystyle r_ {0}}$${\ displaystyle z_ {0}}$

2) (кружок) дает тор с уравнением ${\ displaystyle m_ {0} :( rR) ^ {2} + z ^ {2} -a ^ {2} = 0, R> a> 0 \,}$

${\ displaystyle (x ^ {2} + y ^ {2} + z ^ {2} + R ^ {2} -a ^ {2}) ^ {2} -4R ^ {2} (x ^ {2} + y ^ {2}) = 0 \.}$

3) ( кривая Кассини ) дает площадь по уравнению ${\ displaystyle m_ {0} :( r ^ {2} + z ^ {2}) ^ {2} -2c ^ {2} (r ^ {2} -z ^ {2}) - (a ^ {4 } -c ^ {4}) = 0, a> 0, c> 0 \,}$

${\ displaystyle (x ^ {2} + y ^ {2} + z ^ {2}) ^ {2} -2c ^ {2} (x ^ {2} + y ^ {2} -z ^ {2} ) - (a ^ {4} -c ^ {4}) = 0}$

(

Лемниската ) была выбрана для картины .${\ Displaystyle а = с = 1}$

Гулдинские правила

Первое правило Гульдина , названное в честь швейцарского математика Поля Гулдина , значительно сокращает вычисления поверхностей вращения, если центр тяжести линий или областей вращающихся объектов может быть легко идентифицирован с использованием симметрии соответствующей задачи.

Обозначения:

${\ displaystyle A}$ = Площадь

${\ displaystyle L}$ = Длина образующей (линия профиля)

${\ displaystyle R}$ = Радиус окружности центра тяжести

${\ displaystyle r}$ = Радиус вращающейся окружности (примеры торов)

Площадь на поверхности вращения, ось вращения не пересекает образующая равна произведению длины образующей линии (линии профиля) и окружности (центр тяжести круга), который генерируется поворот центра тяжести линии профиля: ${\ displaystyle M}$

${\ Displaystyle A = L \ cdot 2 \ pi R}$

Выраженная как функция функции образующей, площадь получается как: ${\ displaystyle f}$

При вращении вокруг оси x

${\ displaystyle A = 2 \ pi \ int _ {a} ^ {b} f (x) {\ sqrt {1+ \ left [f '(x) \ right] ^ {2}}} \ mathrm {d} Икс}$

С , как координата линия центра тяжести линии и ее линейный элемент может быть найдена ${\ displaystyle \ textstyle R = y_ {s} = {\ frac {1} {L}} \ int _ {L} y \ mathrm {d} L}$${\ displaystyle y}$${\ displaystyle L}$${\ displaystyle \ mathrm {d} L}$

${\ displaystyle A = L \ cdot 2 \ pi R = L \ cdot 2 \ pi \ cdot {\ frac {1} {L}} \ int _ {L} f (x) \ mathrm {d} L = 2 \ пи \ int _ {L} f (x) \ mathrm {d} L}$,

что и представляет собой результат выше, если пределы интервала все еще используются. ${\ displaystyle \ textstyle \ mathrm {d} L = {\ sqrt {(\ mathrm {d} x) ^ {2} + (\ mathrm {d} y) ^ {2}}} = {\ sqrt {1+ \ left ({\ frac {\ mathrm {d} y} {\ mathrm {d} x}} \ right) ^ {2}}} \ mathrm {d} x}$${\ displaystyle x}$${\ Displaystyle [а, б]}$

При вращении вокруг оси Y

${\ displaystyle A = 2 \ pi \ int _ {\ min (f (a), f (b))} ^ {\ max (f (a), f (b))} f ^ {- 1} (y ) {\ sqrt {1+ \ left [\ left (f ^ {- 1} (y) \ right) '\ right] ^ {2}}} \ mathrm {d} y}$

Как и в случае с вычислением объема выше, расчет для непрерывных и строго монотонных участков, в которых существует обратная функция, также должен выполняться отдельно. ${\ displaystyle f (x)}$

Пример: поверхность вращающегося тора :

${\ displaystyle A = 2 \ pi r \ cdot 2 \ pi R = 4 \ pi ^ {2} rR}$

Параметрическая форма

Если кривая определяется ее параметрической формой в интервале , площади поверхностей вращения, которые создаются путем вращения кривой вокруг оси x или оси y, задаются выражением${\ Displaystyle (х (т), у (т))}$ ${\ Displaystyle [а, б]}$

${\ displaystyle A_ {x} = \ int _ {a} ^ {b} 2 \ pi y \, {\ sqrt {\ left ({\ frac {\ mathrm {d} x} {\ mathrm {d} t}) } \ right) ^ {2} + \ left ({\ frac {\ mathrm {d} y} {\ mathrm {d} t}} \ right) ^ {2}}} \, \ mathrm {d} t}$

${\ displaystyle A_ {y} = \ int _ {a} ^ {b} 2 \ pi x \, {\ sqrt {\ left ({\ frac {\ mathrm {d} x} {\ mathrm {d} t}) } \ right) ^ {2} + \ left ({\ frac {\ mathrm {d} y} {\ mathrm {d} t}} \ right) ^ {2}}} \, \ mathrm {d} t}$

Типы

Поверхности вращения постоянной гауссовой кривизны были классифицированы Карлом Фридрихом Гауссом и Фердинандом Миндингом . Поверхности вращения с исчезающей гауссовой кривизной - это плоскость, цилиндр и конус. Поверхности вращения с положительной гауссовой кривизной - это сферическая поверхность, поверхности шпиндельного типа и поверхности бусиного типа. Поверхности вращения с отрицательной гауссовой кривизной - это псевдосфера , также известная как поверхность Миндинга, поверхности конического типа и поверхности типа долины. Сферическая поверхность и псевдосфера имеют постоянную гауссову кривизну.

Смотри тоже

• Твердая революция
• Внешняя поверхность

литература

• W. Kühnel: Differentialgeometrie , Vieweg-Verlag, Braunschweig / Wiesbaden, 2003, ISBN 3-528-17289-4 , стр. 52
• Манфредо Пердигау ду Карму: Дифференциальная геометрия кривых и поверхностей. Prentice-Hall Inc., Верхняя река Сэдл, штат Нью-Джерси, 1976, ISBN 0-13-212589-7 .
• Малая энциклопедия математики , Harri Deutsch-Verlag, 1977, стр. 621
• Майкл Спивак : Всестороннее введение в дифференциальную геометрию (том 3) , Publish or Perish Press, Беркли, 1999, ISBN 0-914098-72-1
• Карл Штрубекер : Дифференциальная геометрия (Том III) , Коллекция Гёшена, Том 1180, De Gruyter, Берлин, 1959
• Поверхности вращения и линейчатые поверхности (файл PDF; 777 kB) с формулами для расчета кривизны и примерами поверхностей вращения

Индивидуальные доказательства

1. ↑ Равиш Р. Сингх, Мукул Бхатт: Инженерная математика . Обучающий подход. Тата МакГроу Хилл, Нью-Дели 2010, ISBN 978-0-07-014615-0 , стр. 6.90 (английский, ограниченный предварительный просмотр в Поиске книг Google).