Удвоение куба
Удвоение куба , также известный как проблема Делосы , относится к геометрической задаче данного куба второй куба с удвоенным объемом к конструкции . Задача принадлежит к трем « классическим задачам античной математики » и возникла уже в V веке до нашей эры. До н.э. в Древней Греции сформулировано.
Первоначальный куб с длиной ребра (так называемый единичный куб ) имеет объем. Другой куб имеет длину ребра и объем . Новая длина ребра - это кубический корень из , то есть . Это может быть определено как предельное значение подходящих последовательностей , но не может быть построено за конечное число шагов из расстояний 0 и 1 с использованием циркуля и линейки . Если вы попытаетесь поработать над проблемой удвоения куба исключительно с помощью вспомогательных средств, которые Евклид использовал в своих элементах , а именно с помощью циркуля и линейки без опознавательных знаков, решить эту проблему невозможно. Это утверждение может быть переведено на технический язык алгебры , тем самым, наконец, может быть дано математическое доказательство невозможности построения. Одно из таких исследований было впервые выполнено французским математиком Пьером Ванцелем в 1837 году. Однако весьма вероятно, что Карл Фридрих Гаус уже знал доказательство ранее, но не записал его.
Идентичные проблемы возникают, когда объем куба увеличивается в 3, 4, 5, 6 и 7 раз от исходного объема. С другой стороны, задача, например, восьмикратного увеличения объема не является проблемой, потому что кубический корень из 8 может быть вычислен без каких-либо проблем, а результирующее удвоение длины ребра легко сделать.
Если ограничение ослаблено и допускается дополнительная помощь, например, соответствующие отметки на линейке или специальные кривые, то возможно построение куба с удвоенным объемом. Соответствующие процессы были известны еще в древности .
История с древности
Самым важным древним источником об удвоении куба является комментарий покойного античного автора Евтокиоса к работе Архимеда «О сфере и цилиндре» (« Περὶ σφαίρας καὶ κυλίνδρου Peri sphairas kai kylindrou »), в котором различные подходы древних математиков собраны. Среди прочего, там дословно цитируется письмо ученого Эратосфена (около 275-194 гг. До н.э.) царю Птолемею (вероятно, Птолемею III или Птолемею IV ), которое, как теперь доказано, является подлинным воспроизведением исходного письма и в который ученый обращается к правителю по вопросу об удвоении игральных костей. В качестве старейшего доказательства этой математической проблемы Эратосфен цитирует «одного из старых поэтов- трагедий» (« τῶν ἀρχαίων τινὰ τραγῳδοποιῶν tōn archaiōn tina tragōdopoiōn »), в работе которого мифический царь Минос дважды построил гробницу своего сына Глаукуку. как первый набросок, но сохраните форму куба. Из трех важных афинских поэтов-трагедий V века до н.э. До н.э. - Эсхил , Софокл и Еврипид - мы знаем, что они взяли легенду о Миносе и Главке в одном из своих произведений; однако не исключено, что это цитата из трагедии совершенно другого поэта.
Альтернативное название «Delisches Problem» восходит к эпизоду, который Эратосфен также цитирует в своем письме, но который также описывается различными другими древними авторами (включая Плутарха и Теона Смирнского ) и который, с точки зрения древних ученых, является Основанный на реальном историческом событии, может: жители острова Делос попросили у оракула совета во время серьезной эпидемии о том, что они могут сделать, чтобы улучшить свое положение. Оракул велел им увеличить вдвое размер кубического алтаря в храме Аполлона на острове, то есть его объем . Однако делосские архитекторы не понимали, как это можно сделать на самом деле, и затем попросили совета у Платона (428 / 427–348 / 347 до н.э.). Он направил их к Архиту из Таранто , Евдоксу из Книдоса и Менахмосу , каждый из которых открыл разные подходы к решению. Однако, согласно Плутарху, Платон критиковал их подходы, потому что, по его мнению, с помощью механических методов они разрушают «добро» и элегантность геометрии. Интересно, что в комментарии Евтокия к Архимеду Платон также приписывает собственное механическое решение проблемы Делика (см. Раздел «Механический метод Платона» ). Если не иметь в виду Платона, отличного от известного философа, преобладающее мнение исследователей предполагает, что это неправильная атрибуция.
Подобные проблемы со строительством алтарей (но с проблемой удвоения квадрата вместо куба) существовали в ведические времена в Индии, и они вызвали математические дискуссии ( Сульбасутры ). С помощью квадрата проблему удвоения можно решить с помощью теоремы Пифагора .
Старинные решения с дополнительными инструментами
- Гиппократ Хиосский (вторая половина V века до нашей эры) первым продемонстрировал решительный подход к теоретическому решению проблемы. Он обнаружил: проблема удвоения куба эквивалентна задаче определения двух средних пропорций двух величин . Это означает, что для маршрута мы ищем два маршрута и поэтому
- Это влечет за собой .
- Архит Тарантский (435 / 410–355 / 350 до н.э.) был первым, кто реализовал вышеупомянутую теорему Гиппократа с помощью кривой, названной в его честь; описано в разделе Кривая архита .
- Платон (428 / 427–348 / 347 до н.э.) был назван Евтокиосом первым, кто нашел механический метод решения удвоения куба . Как уже было сказано выше, это решение не должно исходить от него.
- Сообщается, что Евдокс (397 / 390–345 / 338 до н.э.) нашел решение, построив две средние пропорции с помощью неизвестных кривых и их точек пересечения.
- Menaichmos (около 380-320 г. до н.э.) найдены два решения: одно , в котором парабола пересекаются с помощью гиперболы , а второй, подробно описано в разделе Использование параболы , как пересечение двух парабол.
- Эратосфен (около 278–194 до н.э.) описывает в своем письме царю Птолемею после его введения в историю делосской проблемы свой собственный «механический метод» с использованием аппарата, который он назвал «мезолабе».
- Диоды (.. в 240–180 гг. До н.э.) использовали названные в его честь цизоиды раствора ; описан в разделе Циссоиды Диокла .
Доказательство неразрешимости с помощью циркуля и линейки
История доказательств
По сути, математики древности не просто использовали циркули и линейки для решения задач. Предположение о существовании такой методологической ограниченности оказалось современным мифом. В 1837 году Пьер Ванцель доказал, что задача на самом деле неразрешима, используя только циркуль и линейку. Его доказательство было основано на следующих алгебраических соображениях:
- 1. В первой части доказательства он утверждает, что, если проблема проектирования может быть решена с помощью линейки и циркуля, «неизвестное значение проблемы может быть получено путем решения серии квадратных уравнений, коэффициенты которых являются рациональными функциями параметров. из этой проблемы и корней предыдущих уравнений».
С "неизвестным о проблеме" з. Б. имел в виду маршрут, который вы ищете.
- 2. Затем он показал, что каждое алгебраическое число является решением последнего уравнения системы
- есть, где коэффициенты всегда находятся в теле путем последовательного присоединения , всегда решается полиномом степени с коэффициентами в . Это решает уравнение и являются заданными параметрами проблемы.
- 3. Ванцель знал, что каждое алгебраическое число является решением многочлена со степенью двойки, если оно выбрано достаточно большим. Следовательно, его основной результат состоял в том, чтобы показать, что если число требуемых уравнений было сведено к минимуму, полученный многочлен неприводим над .
Невозможность построения следует теперь как следствие из предложений 1–3: если бы, начиная с единичного куба, можно было бы построить удвоение куба с помощью циркуля и линейки, то должен был бы существовать нуль неприводимого куба. многочлен со степенью двойки. Многочлен неприводим над , но имеет степень 3. Противоречие.
Следует отметить, что оригинальная публикация Ванцеля рассматривается математиком Йеспером Лютценом как неполная и трудная для понимания - прежде всего это относится к «доказательству» основного предложения 3. После этого Люцен закрыл пробелы, и результаты, как описано выше, сформулированы в современный технический язык. Доказательство Ванцеля о невозможности построения удвоения куба и тройного деления угла с помощью линейки и циркуля было забыто почти на столетие после его публикации в 1837 году. По словам Люцена, «отсутствие дурной славы автора», «тот факт, что некоторые из его современников считали результат известным или даже доказанным», и что «результат не считался важным математическим результатом во время его публикация »движущие причины.
Историки сомневаются, что Ванцель был первым, кто узнал об доказательствах , поскольку у молодого Карла Фридриха Гаусса, скорее всего, они были. Большая часть его работы Disquisitiones arithmeticae , опубликованной в 1801 году, посвящена вопросу, каким условиям должно удовлетворять полиномиальное уравнение , чтобы его можно было решить с помощью квадратных радикалов. Там же вы найдете предложения, названные в честь Гаусса, с помощью которых можно продемонстрировать неразрешимость большинства классических задач с помощью циркуля и линейки. С помощью разработанных им методов Гаусс доказал, например, что 17-угольную диаграмму можно построить с помощью циркуля и линейки. Историки математики Кристоф Скриба и Питер Шрайбер объясняют тот факт, что, несмотря на это, Ванцель назван и цитируется многими авторами как создатель предложений, «коммуникативным трудностям» науки XIX века .
На современном техническом языке доказательство представляет собой приложение всеобъемлющей теории Галуа (после Эвариста Галуа , французского математика) и по существу сводится к тому факту, что иррациональное число не может быть выражено целыми числами , а также четырьмя основными арифметическими операциями, а также не квадратными корнями .
Алгебраическое доказательство

Детальное доказательство невозможности можно провести, используя следующие идеи из алгебры . Пусть имеется набор точек ( комплексных чисел ), содержащих не менее 0 и 1, и произвольная точка . Для этих соображений важно, чтобы комплексные числа можно было понимать как плоскость - в отличие от этого, действительные числа понимаются просто как прямая линия. Затем он применяет , что точка может быть построен из точек с компасом и линейкой , если и только если он находится в теле (здесь находится тело комплексных чисел), который создается за счет придаток квадратного корня из тела
появляется. Грубо говоря, это сумма, которая возникает в результате образования всех сумм, произведений и частных из рациональных чисел . Вот набор комплексно сопряженных к, а символ обозначает объединение двух наборов. Прибавление квадратного корня означает, что должно быть такое, что . Например, сложение квадратного корня из рациональных чисел показывает, что это рациональное число - соответственно, это набор всех сумм, произведений и частных рациональных чисел с этим числом . Когда есть так называемое расширение поля . Проблема удвоения куба с помощью циркуля и линейки может быть сведена к вопросу о том, находится ли число в частичном поле , которое может быть получено путем последовательного сложения квадратных корней. Тем не менее, это означает , что степень расширения в от степени 2 должен быть. Но это
что делает невозможным удвоение куба циркулем и линейкой. То , что расширение тела степени 3 можно увидеть следующим образом : Полином является неприводимым над целыми числами и имеет самый высокий коэффициент 1. Согласно лемме Гаусса, является то уже неприводимым над полем рациональных чисел. Это уже имеет минимальный многочлен от и степень 3. Это приводит к знанию того, что каждый элемент множества , состоящий из всех рациональных чисел, произвольно «смешанных» с кубическим корнем из 2 с помощью основных арифметических операций, является однозначно как рациональные числа могут быть записаны. Например, это
Это становится трёх- мерное векторное пространство над .
Тот же аргумент можно использовать, чтобы показать, что даже умножение куба на натуральный множитель , не являющееся числом куба, не может быть достигнуто с помощью циркуля и линейки.
Геометрические конструкции с механическими приспособлениями
Если вы возьмете другое механическое вспомогательное средство в дополнение к классическим (евклидовым) инструментам, циркулям и немаркированным линейкам, например, специальный механический инструмент или линейку с соответствующей маркировкой, длина ребра куба, необходимая для удвоения куба, теоретически может быть представлена точно.
С помощью отмеченной линейки
Конструкции с помощью так называемой вставки , также известной как конструкции Neusis , используют циркуль, а также линейку, на которую наносится специальная разметка в качестве дополнительного средства.
- Следующая конструкция Нойсиса, которую Генрих Дёрри называет конструкцией из бумажной ленты , является одной из самых известных.
- Если обозначить - как показано на рисунке 1 - край (сторону) начального куба значком , сначала будет построен равносторонний треугольник с углами . Затем следует удвоение линии, от которой получается пересечение, и теперь линия от удлиняется. Затем половина линии будет обращено с помощью . Теперь поместите линейку, отмеченную точкой (расстояние от угла до точки соответствует ) на чертеже. Поверните и сдвиньте линейку до тех пор, пока ее угол не окажется на продолжении линии , маркер точки - на продолжении линии, а край линейки не будет проходить через точку . Наконец, соедините точку с
- Отрезок - это длина края куба, который вы ищете, с удвоенным объемом исходного куба.
- Менее известная конструкция Neusis исходит от Исаака Ньютона (рис. 2), но примечательна своей простотой.
- Он начинается с установления вертикальной линии на полупрямой . Угловая опора с угловой шириной на вершине следующим образом . Теперь поместите линейку, отмеченную точкой (расстояние от угла до точки соответствует краю начального куба) на чертеже. Поверните и сдвиньте линейку до тех пор, пока угол линейки не окажется на ножке угла, отметка точки будет на полупрямой линии, а край линейки пройдет через острие . Наконец, соедините точку с Нарисованной точкой только для того, чтобы ее было легче сформулировать в следующем доказательстве.
- Отрезок - это длина края куба, который вы ищете, с удвоенным объемом исходного куба.
- Доказательство правильности
- На рисунке 2 показано, что прямоугольные треугольники (синий) и (зеленый) похожи друг на друга из-за угла при вершине ,
- следовательно, применяется в соответствии с законом 2-го луча
- (1)
- прямоугольный треугольник и касательная
- (2)
- Части уравнения (2) в квадрате
- (3)
- преобразованные результаты
- (4)
- Прямоугольный треугольник по теореме Пифагора
- (5)
- Значение (5) вставлено в (4)
- (6)
- (6)
- преобразованные результаты
- (7)
- после упрощения
- (8-е)
- это окончательно следует из этого
- (9)
- Прописью:
- Объем куба с длиной ребра равен удвоенному объему исходного куба с длиной ребра.
Определение двух средних пропорций с помощью механического инструмента
Использование двух механических инструментов, описанных ниже, обеспечивает так называемые две средние пропорции и Гиппократа Хиосского. Они нужны для удвоения стартового куба с длиной ребра . Среднее пропорциональное соответствует искомой длине ребра удвоенного куба.
- Теорема Гиппократа Хиосского описана в разделе « Построение специальных кривых» .
Платоновский механический метод
Как упоминалось во введении, Евтокий называет Платона первым, кто использовал следующий метод для решения проблемы удвоения куба. Современные комментаторы отрицают это Платон из-за его яростного неприятие механических средств, но Латтманн в своем исследовании Математическое моделирование у Платона между Фалесом и Евклидом в 2019 году подробно описывает, почему решение можно по праву приписать Платону.
«Вопреки общему мнению , очевидно, что анекдот о делосской проблеме не является ни полностью, ни частично вымышленным, но, по всей вероятности, исторически верен. На этом основании, на втором этапе, подход к проблеме Делика, приписываемый Платону в традиции, может быть рассмотрен как потенциально подлинное, хотя и косвенно переданное, свидетельство Платона ».
Механический инструмент (без спецификации материала ) имеет вид прямоугольной рамы. Две боковые части рамы перпендикулярны более длинному базовому элементу. Чтобы свободную линейку можно было перемещать точно параллельно своей противоположной стороне, она направляется соответственно в двух боковых частях. Для большей наглядности инструмент показан в супервизоре . На соседнем рисунке использованы оригинальные, частично греческие обозначения точек.
метод
Во-первых, две заданные переменные и нарисованы перпендикулярно друг другу и с продолжением от точки .
Теперь инструмент перемещается по чертежу следующим образом (см. Анимацию), пока не будут найдены две средние пропорции :
Внутренний край базового элемента всегда проходит через точку, и точка всегда лежит на продолжении линии до того, как острие линейки будет наложено на продолжение линии .
В результате механический инструмент обеспечивает
- а также
доказательство
Из-за параллельности и четырех прямых углов в вершине следующие треугольники имеют одинаковые углы и, следовательно, похожи друг на друга:
Поскольку вершина имеет прямой угол, следующие углы совпадают:
Евклид, стихии, 1, 32:
Поскольку вершина имеет прямой угол, следующие углы также совпадают:
Согласно Евклиду, элементы 6, 4 пропорции следующие:
Механический метод Эратосфена
Эратосфен из Кирены изобрел (на основе теоремы Гиппократа) механический инструмент, который он описал в письме царю Птолемею как один:
«[...] механическое устройство для определения, с помощью которого мы не только найдем две средние пропорции между двумя заданными прямыми линиями, но и столько, сколько сможем найти».
Механическое устройство можно представить в виде коробки , изготовленную из дерева, бронзы или слоновой кости с тремя очень тонкими таблетками в виде одинаковых прямоугольных треугольников, которые могут быть перемещены вправо или влево , с помощью канавок. В задаче, в которой ищутся более двух средних пропорций для двух переменных, необходимое количество треугольников всегда на один больше, чем количество искомых средних пропорций. Эратосфен придумал решение удвоить куб, высеченный в камне в храме Птолемеев в Александрии.
Механическое устройство, изображенное в абстрактной форме на диаграмме напротив - как его называет Эратосфен - показывает два параллельных луча, и они символизируют двух правителей. Между линейками есть три прямоугольных треугольника, первый фиксируется в точке, а два других направляются так, чтобы их можно было перемещать. В качестве альтернативы также возможны три прямоугольника с нарисованными диагоналями. Вертикально нарисованные треугольники имеют переменную высоту и небольшую ножку произвольно выбираемой длины (на схеме ). Длина второй переменной отображается как расстояние на слишком вертикальной линии в точке третьего треугольника . Луч (не показан) из точки сквозь прорезание врезается в линию , создает путь и, таким образом, раскрывает основную идею устройства, а именно теорему о лучах .
метод
Требуется всего несколько шагов, например B. второй треугольник (синий) и третий треугольник (желтый) можно перемещать между линейками следующим образом, пока не будут найдены две средние пропорции и (см. Анимацию):
Всегда перемещайте второй треугольник (синий) по направлению к первой точке так, чтобы его гипотенуза , прямая (красная) и вертикальная линия пересекались в этой точке . Только на следующем шаге толкайте третий треугольник (желтый) так, чтобы его гипотенуза , прямая (красная) и вертикальная линия пересекались в точке . Повторение этих шагов дает две средние пропорции и
доказательство
Если два балки , или в режется, то
а также
- ,
в то время как
по этой причине
Похожий
Таким образом, и находятся в непрерывной пропорции, как и две средние пропорции.
Строительство с использованием специальных кривых
Если куб, имеющий длину ребра относительно его объема с удвоенной длиной ребра большего куба, следующее применяется для определения двух средне-пропорциональных и Гиппократа множества Хиос:
Если исключить , результат будет:
из этого следует:
- (1)
Если исключить , результат будет:
из этого следует:
- (2)
Из-за особой степени сложности - трехмерности, первая половина IV века до нашей эры. BC - решение проблемы с помощью кривой Archytas подробно описано ниже.
Кривая Архита

Это характеризуется пересечением (зеленый цвет) двух кривых проникновения, которые создаются взаимодействием трех фигур: полуцилиндра с кривой Архита (красная пунктирная линия), восьмой части вращающегося тора ( антрацит ) и конического сечения. (желтый) с треугольной поверхностью среза (синий). диаметр
За несколько десятилетий до Архита Гиппократ Хиосский сумел удвоить куб, проследив его до проблемы построения пропорций. Архиту из Таранто удалось их теоретическое построение с помощью специальной кривой, названной в его честь. Следующие три рисунка необходимы для их визуализации или применения (см. Схему рядом):
- Полуцилиндр , стоит на полукруге с радиусом и диаметром . Высота полуцилиндра составляет прибл.
- Восьмая часть так называемого тора вращения без «дыры» с радиусом
- Сечение конуса, взятое из конуса с радиусом и высотой , с треугольником в качестве его пересечения. Сечение конуса достигает своего максимального размера, а именно четверти общего конуса, когда треугольник охватывает угол с треугольником и, таким образом, лежит на прямоугольной поверхности полуцилиндра.
Кривая Архита - это так называемая кривая пересечения, которая возникает, когда полуцилиндр проходит через одну восьмую вращающегося тора без «дыры». Как видно на диаграмме, четверть конуса проходит через две соседние фигуры и тем самым создает вторую кривую пересечения, которая пересекается с кривой Архитаса.
Эти две средних пропорций встречаются , когда гипотенуза в (синей) треугольной секции конуса пересекает кривой Архит в (зеленый) точке . Точка лежит на боковой поверхности полуцилиндра (на кривой Archytas), на треугольной поверхности среза конического сечения и на полукруглой поверхности среза вращающегося тора без «отверстия».
Геометрическое рассмотрение
Соседний рисунок и аналогичный рисунок в следующем разделе показывают геометрический подход, который Archytas использовал для описания кривой, которую он нашел, с помощью двух средних пропорций . Фигура состоит, среди прочего, из. из двух прямоугольных , подобных треугольников и каждый из которых имеет круг Thales . Полукруг, стоящий перпендикулярно основанию полуцилиндра и вращающийся вокруг точки - с двумя средними пропорциями и - имеет диаметр диаметра полуцилиндра (см. Кривую изображения Archytas).
Со вставленными значениями из (1) и (2), согласно Гиппократу Хиосскому, применимо следующее:
- (3)
- (4)
Применяются следующие условия маршрута:
- (5)
- (6)
Построение длины ребра сдвоенного куба

Для наглядности тор вращения показан в разделе Curve of Archytas . Достигнутая в анимации , это соответствует геометрическому подходу Archytas, показанному на небольшом эскизе. Анимация, между 15 с и в конце 25 с перерыв. Посмотреть анимацию строительства
Так называемое программное обеспечение динамической геометрии (DGS) используется для графического представления - как на соседнем рисунке .
Он начинается с рисования единичной окружности с диаметром . Последующий радиус , чтобы сократить круг в ее следовать по касательной через и расширение и пересекаются в точке А параллельно выкл сокращений диаметра в и окружности в
Затем рисуется короткая дуга окружности с радиусом, и точка определяется с произвольно выбираемым положением. После соединения точки с , это приводит к точкам пересечения на и на полукруге. Далее следует полукруг вверху, а вертикальная линия в нем дает точку пересечения на полукруге вверху Следующий полукруг вверху и вертикальную линию в в результате получится точка пересечения полукруга через Das. Затем следует возвести полуцилиндр (высота около 2,5) над полукругом .
Он продолжается, рисуя дугу вокруг точки с радиусом, который она врезает в продолжение края полуцилиндра, к которому ведет. Теперь точка соединена с. Линия, проведенная от точки к дуге, образует точку пересечения. Соединение с создает треугольник, конгруэнтный треугольнику. Это возможно, потому что полукруг вверху и четверть круга параллельны друг другу. Глядя на контекст, два также совпадающих треугольника и дуга вокруг, поскольку площадь представляет собой конус, общая сумма которого должна быть распознана. После соединения точек с и с двумя соответствующими прямоугольными треугольниками и, наконец, результатом
Полукруг - поверхность среза не показанного Rotationstorus без "отверстия" - теперь должен быть повернут против часовой стрелки, пока не появится гипотенуза также, но по часовой стрелке, треугольника, полукруга в разрезах. Следует отметить, что линии и расположены перпендикулярно друг другу. Согласно теореме Евклида о высоте это приводит к
Отсюда следует, что угол в этом положении такой же . Эти четыре треугольника , и , и , следовательно , похожи друг на друга. Отрегулированное таким образом расстояние соответствует искомой длине ребра удвоенного куба, см. Выше.
Во время вращения полукруга точка в треугольнике определяет (красную) кривую Архита на поверхности полуцилиндра.
- Для точной точки остановки (точка пересечения гипотенузы треугольника ) анимированного поворота полукруга на расстоянии определяется с помощью DGS.
С помощью парабол

Менахмос решил проблему построения двух требуемых средних пропорций как пересечение двух конических сечений (на основе преобразования задачи Гиппократом).
Иоганн Кристоф Штурм пишет об этом :
( типографически нормализовано )
" Разрешение.
Итак, теперь есть две прямые AB и BC, между которыми
должны быть найдены две средние линии с одинаковым поведением / поэтому поместите две заданные линии под прямым углом друг на друга /
и продолжите их в направлении D и E без меры. /; Затем опишите /, как требуется
линией BC, umb BE параболой / (то есть /, что пересечение - это линия,
проведенная вертикально от ее контура до линии BE / (как здесь пересечение EF), равно правому
ekk от BC и bem [часть] средней линии между B и предыдущей вертикалью (здесь BE),
см. Примечание ниже: Опять же, опишите / предыдущие размеры / umb BD,
если линия AB требует другой параболы / и от точки F, в которые,
если они прорежут друг друга / проведут вертикальные линии FD и FE, то BE и BD будут желанными
двумя средними, одинаково ведущими себя ".
Циссоида Диокла
Диокл решил проблему двух средних пропорций с помощью кривой, названной в его честь, также известной как кисоиды Диокла .
Если обозначить две пропорции с помощью и, то в результате будет решаемая конструкционная проблема «двойная пропорция между a и 2a».
Это длина стороны, которую вы ищете (отмечена на рисунке 2 ), она применяется
- Предварительное рассмотрение
В декартовы координаты в cissoids являются г. Б.
Конструкция упрощается, если значение множителя в декартовых координатах зиссоидов равно длине ребра исходного куба . Требуется только та часть графика циссоидов, которая находится в 1-м квадранте декартовой системы координат.
- метод
Пусть это будет начало координат, центр полукруга с любым радиусом и диаметром.
Для того, чтобы определить точку на cissoid (см. Рис.1), вам нужны две параллели и которые перпендикулярны к диаметру и на одинаковом расстоянии от центра . После продолжения линии за ее пределы , полупрямая, проведенная от сквозной до продолжения, создает пересечение на циссоиде.
Непрерывное изменение расстояния между двумя параллелями и друг другом генерирует график циссоидов в 1-м квадранте с помощью перемещаемой точки в начале координат .
Он продолжается (см. Рис. 2) с тем, что на диаметре перпендикулярное расстояние, имеющее длину, равную соединению точки с пересекается график цисоида в конечном соединении точки с поставками с запрошенной страницей удвоенного куба.
Линия, проведенная параллельно пунктирной линии, используется только в качестве доказательства.
Итерационное построение аппроксимации кубического корня
По причинам, уже описанным выше, результат кубического корня не может быть точно представлен с помощью циркуля и линейки с конечными шагами построения.
Метод Ньютона позволяет получить очень хорошие приближения . В дальнейшем он используется для представления реального нуля в функции удвоения кубы
может быть достигнуто как приближение с помощью нескольких итерационных шагов.
Может использоваться как начальное значение . Шаги итерации алгоритма проходят через
Определяются.
Поскольку выражение содержит только основные арифметические операции , результат каждого шага итерации может быть построен как сегмент с циркулем и линейкой .
Расчет итерационных шагов
В формуле
член в правой части уравнения дает результат десятого шага итерации. Шаг итерации состоит из шести алгебраических операций , из которых пятая всегда является числителем, а вторая - знаменателем неправильной дроби .
1-й шаг итерации , пять операций имеют, например, Б. использованное значение для
2-й шаг итерации , пять операций имеют, например, Б. использованное значение для
3-й шаг итерации , пять операций имеют, например, Б. использованное значение для
Этот процесс можно повторять сколько угодно раз. Имеется квадратичная скорость сходимости , что делает метод сравнительно эффективным.
Строительство с компасом и линейкой
Уже после двух шагов итерации эффективность применения метода Ньютона становится очевидной; приблизительное значение, достигнутое до этой точки , теперь является конструктивным продолжением до тех пор, пока на третьем шаге итерации не будет достигнуто приблизительное значение .
Сначала неправильная дробь переформулируется в ( неправильную ) десятичную дробь, а затем отображается в виде точной длины на числовой прямой (рис. 1). Это з. Б. Метод построения десятичного числа с помощью теоремы о 3-м луче . Из-за пропорций это выгодно показать на собственном снимке.
На следующем этапе длина (красный цвет) из рисунка 1 переносится на рисунок 2 (зеленый, цифра 2). За этим следует определение числа квадрата (число 3) и числа куба (число 4). На пятом этапе число куба умножается на коэффициент, и число добавляется. Наконец (цифра 6) определяется частное (красное):
Пример для иллюстрации ошибки
В случае исходного куба с длиной ребра m край только приблизительно удвоенного куба был бы приблизительно на Mm длиннее.
В теории музыки
В теории музыки естественным аналогом удвоения является скачок тона на октаву , то есть музыкальный интервал , возникающий в результате удвоения частоты тона. Естественным аналогом куба (объемом 2) является разделение октавы на три части, каждая с одинаковым интервалом - это три равные стороны куба. В этом смысле проблема удвоения куба решается большой третью при равной настройке . Это музыкальный интервал, составляющий ровно одну треть октавы. Он умножает частоту тона на длину стороны удвоенного куба.
На картинке сбоку изображена главная третья часть нашей эры. Соотношение частот обоих тонов (E: C) точно соответствует .
литература
- Артур Дональд Стил: О роли циркуля и линейки в греческой математике. В кн . : Источники и исследования по истории математики. Отдел B, том 3, 1936 г., стр. 287-369 ( harvard.edu [PDF; 8,8 МБ]).
- Клаас Латтманн: Математическое моделирование Платона между Фалесом и Евклидом (= Наука, технология и медицина в древних культурах. Том 9). Вальтер де Грюйтер, Берлин / Бостон, 2019, стр. 177–270 ( ограниченный предварительный просмотр в поиске книг Google).
- Маркус Аспер : Математика. Греческая математика до конца эллинизма. В: Бернхард Циммерманн , Антониос Ренгакос (Hrsg.): Справочник по греческой литературе древности. Том 2: Литература классического и эллинистического периодов (= Справочник классических исследований . Том 7.2). CHBeck, Munich 2014, pp. 459–481 ( предварительный просмотр в поиске книг Google).
- Йеспер Лютцен: Почему Вантцеля целое столетие упускали из виду? Изменение важности результата невозможности. В: Historia Mathematica . 36, 2009, стр. 374-394, DOI : 10.1016 / j.hm.2009.03.001 .
веб ссылки
Индивидуальные доказательства
- ↑ См. Английский перевод с комментариями: Ревиль Нетц : Работы Архимеда. Переведено на английский язык вместе с комментариями Евтокия, с комментариями и критическим изданием диаграмм. Том 1: Две книги о сфере и цилиндре. Cambridge University Press, Cambridge 2004, ISBN 0-521-66160-9 , здесь стр. 272-306.
- ↑ О подлинности текста письма, написанного Евтокиосом, В. Р. Норр: Древняя традиция геометрических проблем. Бостон 1986, стр. 17-24. По вопросу о том, какой царь Птолемей имеется в виду, см., Например, WR Knorr: Textual Studies in Ancient and Medieval Geometry. Бостон 1989, стр. 144 и далее.
- ^ A b c Reviel Netz: Работы Архимеда. Переведено на английский язык вместе с комментариями Евтокия, с комментариями и критическим изданием диаграмм. Том 1: Две книги о сфере и цилиндре. Издательство Кембриджского университета, Кембридж 2004, ISBN 0-521-66160-9 , стр. 294.
- ^ Ричард Каннихт , Бруно Снелл : Tragicorum Graecorum Fragmenta . 2-е издание. Том 2. Vandenhoeck & Ruprecht, Göttingen 2007, стр. 62, фрагмент Adespota F 166; для обработки материала Glaukos в поэтах-трагедиях см. Georg Weicker : Glaukos 23. В: Paulys Realencyclopädie der classischen Altertumswwissenschaft (RE). Том VII, 1, Штутгарт 1910, полковник 1415 f.
- ↑ Клаас Латтманн: Математическое моделирование на Платоне между Фалесом и Евклидом (= Наука, технология и медицина в древних культурах. Том 9) предоставляет подробный анализ древних источников по анекдоту Делье и возможные исторические основания . Де Грюйтер, Берлин / Бостон, 2019, стр. 187-206; о трех механических подходах и критике Платона, там же, стр. 220–241.
- ^ Ревиел Нец: Работы Архимеда. Переведено на английский язык вместе с комментариями Евтокия, с комментариями и критическим изданием диаграмм. Том 1: Две книги о сфере и цилиндре. Cambridge University Press, Кембридж 2004, ISBN 0-521-66160-9 , стр. 273, примечание 17.
- ↑ Например, Джозеф: Герб павлина. Princeton UP, 2001, стр. 330.
- ↑ а б в г д Хорст Хишер : Мориц Кантор и кривая линия Архита Таранто. (PDF; 1,5 МБ) Saarland University, 2003, p. 74 , по состоянию на 2 декабря 2020 г. (препринт № 86). Печатное издание: Лиза Хефендель-Хебекер , Стефан Хусманн (ред.): Математическая дидактика между предметной ориентацией и эмпиризмом . Festschrift для Норберта Кноха. Franzbecker, Hildesheim / Berlin 2003, ISBN 3-88120-364-8 , стр. 72-83 , с. 74 .
- ↑ a b c Клаас Латтманн: Математическое моделирование у Платона между Фалесом и Евклидом . 5.3 Удвоение куба Платона и механическое доказательство (= Наука, технология и медицина в древних культурах . Том 9 ). Вальтер де Грюйтер, Берлин / Бостон, 2019, ISBN 978-3-11-061382-7 , стр. 215 ff . ( ограниченный предварительный просмотр в поиске Google Книг).
- ^ Франсуа Лассер (ред.): Фрагменты Евдокса из Книдоса. Берлин, 1966, стр. 20-22, 163-166.
- ^ Ревиел Нец: Работы Архимеда. Переведено на английский язык вместе с комментариями Евтокия, с комментариями и критическим изданием диаграмм. Том 1: Две книги о сфере и цилиндре. Издательство Кембриджского университета, Кембридж 2004, ISBN 0-521-66160-9 , стр. 295.
- ↑ a b c d Паскаль Прас, Адриан Де Лонт: Удвоение куба с помощью Kissoiden. Общие кисоиды, семинар по высшим изгибам. Университет Майнца, 2016, стр. 12 , доступ к 5 июля 2021 года .
- ↑ AD Steele: О роли циркуля и линейки в греческой математике. В кн . : Источники и исследования по истории математики, астрономии и физики. Volume B 3, 1936, pp. 287-369 (также конкретно по проблеме удвоения куба).
- ↑ Ванцель: Recherches сюры ль Мойны де reconnaître си ун problème де Geometrie Peut себе résoudre АВЭК ли Règle и др ль КОМПАС (= Журналь де Mathématiques Pures и др appliqué (Журнал Лиувилля) . Том 2 ). 1837, стр. 366-372 .
- ^ Адемар Жан Клод Барре де Сен-Венан : Биография . Вантзель. В: Nouvelles Annales de Mathématiques . Сери 1-й том 7 , 1848, ZDB -ID 426713-8 , стр. 321–331 , стр. 329: Публикации в Journal des mathématiques pures (французский, numdam.org [PDF; 780 кБ ; по состоянию на 10 апреля 2021 г.]).
- ↑ Йеспер Лютцен: Почему Вантцеля целое столетие упускали из виду? Изменение важности результата невозможности. В: Historia Mathematica . 36, 2009, стр. 378-379.
- ↑ Йеспер Лютцен: Почему Вантцеля целое столетие упускали из виду? Изменение важности результата невозможности. В: Historia Mathematica. 36, 2009, с. 379.
- ↑ Йеспер Лютцен: Почему Вантцеля целое столетие упускали из виду? Изменение важности результата невозможности. В: Historia Mathematica. 36, 2009, с. 391.
- ↑ Йеспер Лютцен: Почему Вантцеля целое столетие упускали из виду? Изменение важности результата невозможности. В: Historia Mathematica. 36, 2009, с. 387.
- ↑ Кристоф Дж. Скриба, Питер Шрайбер: 5000 лет геометрии. 3. Издание. Springer-Verlag, Берлин / Гейдельберг 2010, ISBN 978-3-642-02361-3 , стр.405.
- ↑ Фалько Лоренц: Алгебра Том I: Теория полей и Галуа , Springer, стр. 6-13.
- ^ A b Клаас Латтманн: Математическое моделирование Платона между Фалесом и Евклидом . 5.3 Удвоение куба Платона и механическое доказательство (= Наука, технология и медицина в древних культурах . Том 9 ). Вальтер де Грюйтер, Берлин / Бостон, 2019, ISBN 978-3-11-061382-7 , стр. 213 ( ограниченный просмотр в поиске Google Книг).
- ↑ Клаус Фолькерт: История задач геометрического построения I. (PDF; 1,5 МБ) В: Лекция, Кельнский университет в зимнем семестре 06/07; [...] семиугольник. Университет Вупперталь, 2006, стр. 20 , доступ к 15 сентября 2018 года .
- ^ Heinrich Дорри : 35. Delian Куб удвоения проблемы. В кн . : 100 великих задач элементарной математики. Нью - Йорк, Dover Publications, Inc., 1965, стр. 170-171 , доступ к 5 мая 2019 .
- ^ Скип Лестер: История математики. (PDF; 14,2 МБ) 7. Исаак Ньютон (1642–1727) предложил следующую конструкцию для дублирования куба. Университет штата Вашингтон, стр. 11 , доступ к 8 ноября 2019 .
- ↑ а б в Хорст Хишер: Мориц Кантор и кривая линия Архита Таранто. (PDF, 1,5 MB) Саар университет , 2003, стр . 76 , доступ к 30 октября 2020 года .
- ^ Клаас Латтманн: Математическое моделирование Платона между Фалесом и Евклидом . 5.23 Археологическая и историческая перспектива (= Наука, технология и медицина в древних культурах . Том 9 ). Вальтер де Грюйтер, Берлин / Бостон, 2019, ISBN 978-3-11-061382-7 , стр. 199–212 ( ограниченный предварительный просмотр в поиске Google Книг).
- ^ Клаас Латтманн: Математическое моделирование Платона между Фалесом и Евклидом, 5 Платон и проблема Делича, 5.2.4 Заключение. Вальтер де Грюйтер, Берлин / Бостон, 2019, стр. 207, последний абзац ( ограниченный предварительный просмотр в поиске книг Google)
- ↑ Евклид: Элементы Stoicheia . Книга 1, Предложение 29. Издание Opera-Platonis, Markgröningen 2017, p. 17 ( opera-platonis.de [PDF; 469 кБ ; по состоянию на 12 апреля 2021 г.]).
- ↑ Евклид: Элементы Stoicheia . Книга 1, предложение 32-е издание Opera-Platonis, Markgröningen 2017, стр. 19 ( opera-platonis.de [PDF; 469 кБ ]).
- ↑ Евклид: Элементы Stoicheia . Книга 6, предложение 4-го издания Opera-Platonis, Markgröningen 2017, стр. 4 ( opera-platonis.de [PDF; 529 кБ ; по состоянию на 11 апреля 2021 г.]).
- ^ Перевод Клааса Латтмана: Математическое моделирование у Платона между Фалесом и Евклидом. Вальтер де Грюйтер, Берлин / Бостон, 2019, ISBN 978-3-11-061382-7 , стр. 182 ( ограниченный предварительный просмотр в поиске книг Google).
- ↑ Cambridge University Press (Ред.): Работы Архимеда . Комментарий Евтокия к «Сфере и цилиндру II», как у Эратосфена. University Press, Нью-Йорк 2004, ISBN 0-521-66160-9 , стр. 294–298 (английский, ограниченный предварительный просмотр в Поиске книг Google [доступ 10 декабря 2020 г.]).
- ↑ Бартель Леендерт ван дер Варден : Пробуждение науки. 1956, 230 е. Три прямоугольника или треугольника, которые можно было двигать вдоль линейки, одна сторона которых могла свободно вращаться.
- ^ A b Томас Хит: История греческой математики . Дублирование куба, (ζ) Эратосфен. Лента 1 . Кларендон Пресс, Оксфорд 1921, стр. 259 (англ., Скан - Интернет-архив ).
- ↑ а б Хорст Хишер: Мориц Кантор и кривая линия Архита Таранто. (PDF, 1,5 MB) Саар университет , 2003, стр 79 и далее.. , Accessed 1 ноября 2020 года .
- ↑ Рудольф Стопфер: Удвоение куба, 5-е решение по Архитасу. Семинар: Классические проблемы античности. Университет Байройт , 8 июня 1997 года, доступ к 30 октября 2020 .
- ↑ Дидактика математики, Программа динамической геометрии. Университет Вюрцбург , доступ к 4 августа 2021 года .
- ↑ Хорст Хишер: 6.1 Решение: пересечение двух парабол согласно Менахмосу. (PDF; 1,2 МБ) О проблеме удвоения куба на иллюстрации Иоганна Кристофа Штурма 1670. Saarland University, 2015, pp. 9–10 , по состоянию на 1 мая 2019 г. (препринт № 367).
- ↑ Исправление вытекает из контекста предложения.
- ↑ Иоганн Кристоф Штурм: Второй искусственный или геометрический путь ... [ Второй искусственный или геометрический путь ... ] В: Des Несравненные книги ARCHJMEDJS Kunſt. [ Несравненные художественные книги АРХИМЕДИС. ] Nuremberg 1670. DTA Deutsches Textarchiv, p. 118 ff., Здесь p. 119, urn : nbn: de: kobv: b4-20590-8 ( оцифрованный и полный текст в немецком текстовом архиве , по состоянию на 2 ноября 2020 г.) .
- ↑ Паскаль Прас, Адриан Де Лонт: удвоение куба с помощью кисоидов. Общие кисоиды, семинар по высшим изгибам. Университет Майнца, 2016, стр. 9 , доступ к 5 июля 2021 года .
- ↑ man: Элементарная алгебра Aein. В: Docuri. 10 июля 2016 г., стр. 61–63 , по состоянию на 16 декабря 2020 г. (на английском языке).
- ^ Пол Бамберг: дифференцируемость, метод Ньютона, обратные функции. canvas.harvard, 7 июля, 2016, стр. 31 , доступ к 16 декабря 2020 .
- ^ RC Phillips: Равно темперированная гамма. В: Musical Opinion and Music Trade Review. 29 (337), 1905, ZDB -ID 227419-X , стр. 41-42.







![{\ displaystyle {\ sqrt [{3}] {2}} = 1 {,} 259921 \ ldots}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc4058bbfb35a02631b34c9d9449efd8b9952633)
![{\ sqrt [{3}] {2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710)

![{\ Displaystyle а = {\ sqrt [{3}] {2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61b02de6ae656efbfa6bc25257931c87610a93cc)




![{\ Displaystyle х = {\ sqrt [{3}] {2}} \ cdot a}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8806b3b210d5b5b3faab975b558761c2a98cf0fd)

![{\ Displaystyle х = {\ sqrt [{3}] {2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c78fd4e8a5860369203e19242e3b8fc442b2e34)













![{\ displaystyle {\ sqrt [{3}] {2}} = 1 {,} 2599210498948732 ...}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c823b1fddc8d0c81eaec2cf50de97e3f50785c1e)
















![{\ displaystyle [\ mathbb {Q} ({\ sqrt [{3}] {2}}): \ mathbb {Q}] = 3 \ not = 2 ^ {n} \ qquad {\ text {для всех}} \, n \ in \ mathbb {N},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78baa1ec4584c13e6128616e5b344e7b5fa7b87f)
![{\ Displaystyle \ mathbb {Q} ({\ sqrt [{3}] {2}}) | \ mathbb {Q}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5803afab02e9215c8a3525b22d67818bf3ed380b)


![\ mathbb {Q} ({\ sqrt [{3}] {2}})](https://wikimedia.org/api/rest_v1/media/math/render/svg/4682c6f3952f1b35a5db23be9b806fc79e771d30)
![{\ displaystyle a + b {\ sqrt [{3}] {2}} + c {\ sqrt [{3}] {4}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f72434841a928d9a64f39067ea7755fd32a49954)

![{\ displaystyle {\ frac {{\ sqrt [{3}] {2}} + 2} {{\ sqrt [{3}] {2}} - 1}} = 4 + 3 \ cdot {\ sqrt [{ 3}] {2}} + 3 \ cdot {\ sqrt [{3}] {4}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cafd9be4a02089bc5c580ffe97f9be4a2d30a955)
















![{\ Displaystyle {\ overline {CQ}} = к \ cdot {\ sqrt [{3}] {2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/107bcbe2f4a8c54b1ab5860bce100ad6ffa8a14b)


![{\ displaystyle a: x = b: y = c: a = {\ sqrt [{3}] {2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aba0e2e729a1940baffb3949e035ef2489860270)



![{\ Displaystyle {\ overline {AC}} = \ cdot {\ sqrt [{3}] {2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/403c28421871364a981e34dcbacb7888ea8c46a5)


















![{\ Displaystyle а \ cdot {\ sqrt [{3}] {2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3368a7d04c7a3465047ebe3bfded7aeb5d9471ef)












![{\ displaystyle {\ overline {\ Delta E}} = {\ sqrt {y ^ {2} + x ^ {2}}}, \, \, {\ overline {AE}} = {\ sqrt {4a ^ { 2} + y ^ {2}}}, \, \, x = a \ cdot {\ sqrt [{3}] {2}} \, \,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c87101a01f26469ba01373eda008f9df548c485e)
![{\ displaystyle \, \, y = {\ frac {2a} {\ sqrt [{3}] {2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c5c80148d9d5bebacb157da7c9ea025afb91a8c)





![{\ displaystyle {\ overline {B \ Delta}}: {\ overline {B \ Gamma}} = {\ overline {AB}}: {\ overline {BE}} = {\ overline {BE}}: {\ overline {B \ Delta}} = {\ sqrt [{3}] {2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45f179abc6203a1f5c8946bd4bfb1ed372462f4c)






























![{\ displaystyle x = a \ cdot {\ sqrt [{3}] {2}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f55473f21840034b97fcca3d688f344f8f0452ea)
![{\ displaystyle y = {\ frac {2a ^ {2}} {a \ cdot {\ sqrt [{3}] {2}}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4cf7d9ad0bd969c47e54095c5a555721e1c141f3)
![{\ displaystyle y = {\ frac {2a} {\ sqrt [{3}] {2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a8c21a162fe89a90b2e7f4324deb01bf6bdf24b)




















![{\ displaystyle {\ overline {AD '}}: {\ overline {AK}} = {\ overline {AI}}: {\ overline {AM}} = {\ overline {AK}}: {\ overline {AI} } = y: x = {\ sqrt [{3}] {2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a893191ddc339796b29ebb76e3728e4707000f9)
![{\ displaystyle {\ overline {AI}} = {\ sqrt [{3}] {2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f79389e6ab80ff55fb69871045a529940bd9768)







































![{\ displaystyle x: a = y: x = b: y = {\ sqrt [{3}] {2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/126b8b7b2adae65688facbd5d808867a0790f004)



















![{\ Displaystyle v = а \ cdot {\ sqrt [{3}] {2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05a3846f3b93f73c80131a614bdd5edc9a31a3c8)

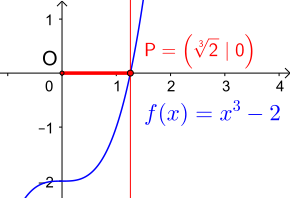








































![{\ displaystyle {\ begin {alignat} {2} {\ text {built length}} \ qquad x_ {3} & = && 1 {,} 259933 \ dots \\ - {\ text {целевое значение}} \ qquad - {\ sqrt [{3}] {2}} & = - && 1 {,} 259921 \ dots \\\ hline {\ text {абсолютная ошибка}} \ qquad F & = && 0 {,} 000012 \ dots \; [\ mathrm {LE}] \ end {alignat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b988acbad6fa40149d3d7ec44e0667b83acb3e8)



![{\ displaystyle ({\ sqrt [{12}] {2}}) ^ {4} = {\ sqrt [{3}] {2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/685fb8afa80ff1c94cfa768b2fe8d06e56248441)